（本题12分）如图，抛物线y=ax²＋bx＋c交x轴于点A（－3，0），点B（1，0），交y轴于点E（0，－3）。点C是点A关于点B的对称点，点F是线段BC的中点，直线l过点F且与y轴平行。直线y=－x＋m过点C，交y轴于D点.
⑴求抛物线的函数表达式；
⑵点K为线段AB上一动点，过点K作x轴的垂线与直线CD交于点H，与抛物线交于     点G，求线段HG长度的最大值；
⑶在直线l上取点M，在抛物线上取点N，使以点A，C，M，N为顶点的四边形是平行四边形，求点N的坐标.

（本题12分）如图，已知抛物线y=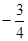x²+3与x轴交于点A、B,与直线y=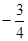x+b相交于点B、C,直线y=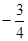x+b与y轴交于点E.
（1）写出直线BC的解析式；
(2)求△ABC的面积；
(3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动（不与A、B重合），同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒，请写出△MNB的面积s与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？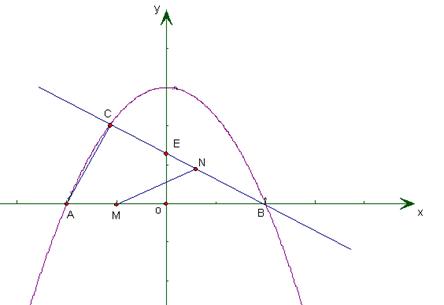

（本题12分）已知两个全等的直角三角形纸片ABC、DEF，如图（1）放置，点B、D重合，点F在BC上，AB与EF交于点G，∠C＝∠EFB＝90°，∠E＝∠ABC＝30°，AB＝DE＝4.

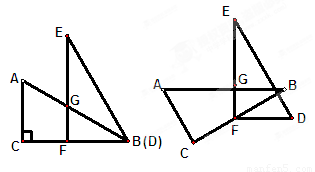
1.（1）求证：△EGB是等腰三角形

2.（2）若纸片DEF不动，问△ABC绕点F逆时针旋转最小            度时，四边形ACDE成为以ED为底的梯形（如图（2）），求此梯形的高。

(本题12分)已知二次函数的图象如图所示．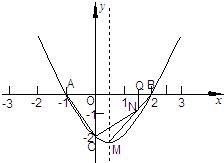

【小题1】（1）求二次函数的解析式及抛物线顶点M的坐标；
【小题2】（2）若点N为线段BM上的一点，过点N作x轴的垂线，垂足为点Q．当点N在线段BM上运动时（点N不与点B，点M重合），设NQ的长为t，四边形NQAC的面积为s，求s与t之间的函数关系式及自变量t的取值范围；
【小题3】（3）在对称轴右侧的抛物线上是否存在点P，使△PAC为直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由；
【小题4】（4）将△OAC补成矩形，使上△OAC的两个顶点成为矩形一边的两个顶点，第三个顶点落在矩形这一边的对边上，试直接写出矩形的未知的顶点坐标（不需要计算过程）．

（本题12分）足球比赛的记分规则为：胜一场得分，平一场得，输一场得分．一去足球队在某个赛季中共需比赛场，现已经比赛了场，输了场，得．请问：

（1）前场比赛中，这去球队共胜了多少场？

（2）这去球队打满场比赛，最高能得多少分？

（3）通过对比赛情况的分析，这去球队打满场比赛，得分不低于分，就可以达到预期的目标，请你分析一下，在后面的场比赛中，这去球队至少要胜几场，才能达到预期目标？