（本题满分10分）

为了解某住宅区的家庭用水量情况，从该住宅区中随机抽样调查了50户家庭去年每个月的用水量，统计得到的数据绘制了下面的两幅统计图．图24－1是去年这50户家庭月总用水量的折线统计图，图24－2是去年这50户家庭月总用水量的不完整的频数分布直方图．

（1）根据图24－1提供的信息，补全图24－2中的频数分布直方图；(3分)

（2）在抽查的50户家庭去年月总用水量这12个数据中，极差是    立方米，众数

是     立方米，中位数是    立方米；(3分)

（3）请你根据上述提供的统计数据，估计该住宅区今年每户家庭平均每月的用水量是多少立方米？(4分)

．（本题满分10分）已知，．

⑴ 当x取何值时，y₁=y₂?  ⑵当x取何值时，y₁比2y₂大3?

（11·永州）（本题满分10分）探究问题：

⑴方法感悟：

如图①，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．

感悟解题方法，并完成下列填空：

将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：

AB=AD,BG=DE, ∠1=∠2，∠ABG=∠D=90°,

∴∠ABG+∠ABF=90°+90°=180°，

因此，点G，B，F在同一条直线上．

∵∠EAF=45°  ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．

∵∠1=∠2，   ∴∠1+∠3=45°．

即∠GAF=∠_________．

又AG=AE，AF=AF

∴△GAF≌_______．

∴_________=EF，故DE+BF=EF．

⑵方法迁移：

如图②，将沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．

⑶问题拓展：

如图③，在四边形ABCD中，AB=AD，E，F分别为DC,BC上的点，满足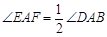,试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）．

（本题满分10分）如图，在平面直角坐标系中，O为坐标原点，P是反比例函数

y＝（x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、

B．

（1）判断P是否在线段AB上，并说明理由；

（2）求△AOB的面积；

（3）Q是反比例函数y＝（x＞0）图象上异于点P的另一点，请以Q为圆心，QO

 半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．

（本题满分10分）已知抛物线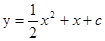与x轴有两个不同的交点．

1.(1) 求抛物线的对称轴；

2.(2) 求c的取值范围；

3.（3）若此抛物线与x轴两交点之间的距离为2，求c的值．