
题目列表(包括答案和解析)
①直接开平方法:对于一元二次方程x2=a(a≥0),因为x是a的平方根,所以x=___________,即x1=___________,x2=___________,这种解一元二次方程的方法叫做直接开平方法.
②配方法:将一元二次方程ax2+bx+c=0(a≠0)配成___________的形式后,当b2-4ac___________时,用直接开平方法求出它的根,这种解一元二次方程的方法叫做配方法.
③公式法:应用一元二次方程ax2+bx+c=0(a≠0)的求根公式x=___________(b2-4ac≥0),这种解一元二次方程的方法叫做公式法.
④因式分解法:若一元二次方程ax2+bx+c=0(a≠0)的左边是关于x的二次三项式易于分解成两个关于x的一次因式乘积的形式时,则方程ax2+bx+c=0可变形为___________,分别令两个一次因式等于0,得两个关于x的一次方程___________和___________,通过解这两个一次方程,就可得原方程的解.这种解一元二次方程的方法叫做因式分解法.
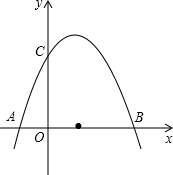 横坐标,此抛物线与y轴的正半轴交于点C.
横坐标,此抛物线与y轴的正半轴交于点C.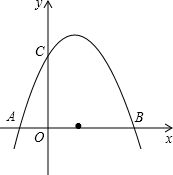 横坐标,此抛物线与y轴的正半轴交于点C.
横坐标,此抛物线与y轴的正半轴交于点C.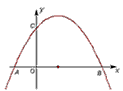
| b |
| a |
| c |
| a |
| 1 |
| x1 |
| 1 |
| x2 |
| 4 |
| x1 |
| 4 |
| x2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com