
题目列表(包括答案和解析)
两条坐标轴直交把平面分为四个象限、四个半轴及一个原点共九个部分,各部分中点的坐标特点(为正、负或0)有所不同.
(1)九部分中的点的坐标特征如何?
(2)填空:
①若M(-m,-m)在第一象限,则F(-m2,-2m)在第________象限.
②若K(a,-b)在第三象限,则L(-a,ab)在第________象限.
③若A1(x,y)在第三象限,则A2(-x,y),A3(-x,-y),A4(x,-y)依次在第________,________,________象限.
④若ab>0,则(a,b)在________象限,若(a,b)在二或四象限,则![]() ________0.
________0.
⑤若ab=0,则点(a,b)必定在________上.
 23、△ABC在平面直角坐标系中的位置如图所示.
23、△ABC在平面直角坐标系中的位置如图所示.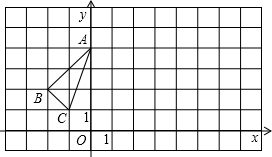
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com