
题目列表(包括答案和解析)
 Q的最大面积;若不存在,请说明理由.
Q的最大面积;若不存在,请说明理由.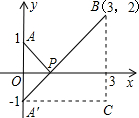 (2012•十堰)阅读材料:
(2012•十堰)阅读材料:| x2+1 |
| (x-3)2+4 |
| x2+1 |
| (x-3)2+4 |
| (x-0)2+12 |
| (x-3)2+22 |
| (x-0)2+12 |
| (x-3)2+22 |
| 2 |
| 2 |
| (x-1)2+1 |
| (x-2)2+9 |
| x2+49 |
| x2-12x+37 |
 阅读材料:
阅读材料:| (x2-x2)2(y2-y1)2 |
| x2+1 |
| (x-3)2+4 |
| x2+1 |
| (x-3)2+4 |
| (x-0)2+(0-1)2 |
| (x-3)2+(0-2)2 |
| (x-0)2+(0-1)2 |
| (x-3)2+(0-2)2 |
| 2 |
| 2 |
| 2 |
| 2 |
| (x-i)2+1 |
| (x-2)2+9 |
| x2+49 |
| x2-12x+37 |
阅读材料:(本题8分)
例:说明代数式  的几何意义,并求它的最小值.
的几何意义,并求它的最小值.
解:  ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离, 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,
只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
所以PA′+PB的最小值为线段A′B的长度.为此,构造直角
三角形A′CB,因为A′C=3,CB=3,所以A′B= ,
,
即原式的最小值为 。
。
根据以上阅读材料,解答下列问题:
(1)代数式 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
(2)求代数式  的最小值
的最小值

阅读材料:
例:说明代数式 x2+1 + (x-3)2+4 的几何意义,并求它的最小值.
解: x2+1 + (x-3)2+4 = (x-0)2+12 + (x-3)2+22 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 (x-0)2+12 可以看成点P与点A(0,1)的距离, (x-3)2+22 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B=3 2 ,即原式的最小值为3 2 .
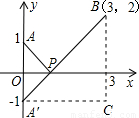
根据以上阅读材料,解答下列问题:
(1)代数式 (x-1)2+1 + (x-2)2+9 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B (2,3)的距离之和.(填写点B的坐标)
(2)代数式 x2+49 + x2-12x+37 的最小值为.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com