
题目列表(包括答案和解析)
(本题12分)如图,抛物线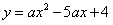 经过
经过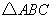 的三个顶点,已知
的三个顶点,已知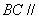
 轴,点
轴,点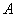 在
在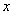 轴上,点
轴上,点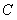 在
在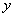 轴上,且
轴上,且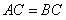 .
.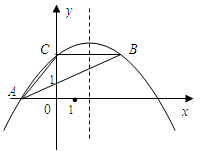
【小题1】(1)求抛物线的对称轴;
【小题2】(2)写出A,B,C三点的坐标(A,B,C三点的坐标只需写出答案),并求抛物线的解析式;
【小题3】(3)探究:若点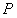 是抛物线对称轴上且在
是抛物线对称轴上且在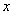 轴下方的动点,是否存在
轴下方的动点,是否存在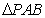 是等腰三角形.若存在,求出所有符合条件的点
是等腰三角形.若存在,求出所有符合条件的点 坐标;不存在,请说明理由.
坐标;不存在,请说明理由.

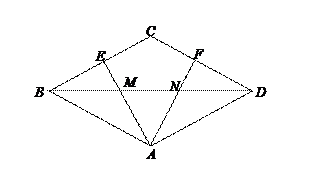
(本题12分)
如图1,已知 ,
, ,
, .
. 是射线
是射线 上的动点(点
上的动点(点 与点
与点 不重合),
不重合), 是线段
是线段 的中点.
的中点.
(1)设 ,
,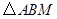 的面积为
的面积为 ,求
,求 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(2)如果以线段 为直径的圆与以线段
为直径的圆与以线段 为直径的圆外切,求线段
为直径的圆外切,求线段 的长;
的长;
(3)连接 ,交线段
,交线段 于点
于点 ,如果以
,如果以 为顶点的三角形与
为顶点的三角形与 相似,求线段
相似,求线段 的长.
的长.
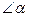 ,当
,当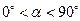 时,连接BE、DF,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.
时,连接BE、DF,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.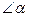 ,当
,当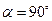 时,连接BE、DF,猜想当AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.
时,连接BE、DF,猜想当AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.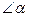 ,当
,当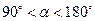 时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.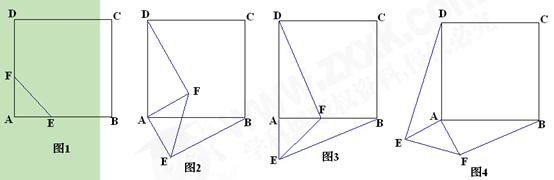
(本题12分)
1.(1)学习《测量建筑物的高度》后,小明带着卷尺、标杆,利用太阳光去测量旗杆的高度.参考示意图1,他的测量方案如下:
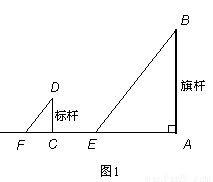
第一步,测量数据.测出CD=1.6米,CF=1.2米, AE=9米.
第二步,计算.
请你依据小明的测量方案计算出旗杆的高度.
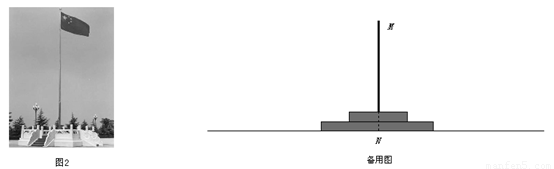
2.(2) 如图2,校园内旗杆周围有护栏,下面有底 座.现在有卷尺、 标杆、平面镜、测角仪等工具,请你选择出必须的工具,设计一个测量方案以求出旗杆顶端到地面的距离.要求:在备用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)你选择出的必须工具是 ;需要测量的数据是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com