
题目列表(包括答案和解析)
课题学习(本题10分)
●探究 (1) 在图1中,已知线段AB,CD,其中点分别为E,F.
①若A (-1,0),B (3,0),则E点坐标为__________;
②若C (-2,2),D (-2,-1),则F点坐标为__________;
(2)在图2中,已知线段AB的端点坐标为A(a,b) ,B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程.
●归纳 无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y) 时,x=_________,y=___________.(不必证明)
★●运用 在图2中, 的图象x轴交于P点。一次函数
的图象x轴交于P点。一次函数 与
与 的图象交点为A,B.
的图象交点为A,B.
①求出交点A,B的坐标(用k表示);
②若D为AB中点,且PD垂直于AB时,请利用上面的结论求出k的值。


 的图象x轴交于P点。一次函数
的图象x轴交于P点。一次函数 与
与 的图象交点为A,B.
的图象交点为A,B.

课题学习(本题10分)
●探究 (1) 在图1中,已知线段AB,CD,其中点分别为E,F.
①若A (-1,0), B (3,0),则E点坐标为__________;
②若C (-2,2), D (-2,-1),则F点坐标为__________;
(2)在图2中,已知线段AB的端点坐标为A(a,b) ,B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程.
●归纳 无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d), AB中点为D( x,y) 时,x=_________,y=___________.(不必证明)
x,y) 时,x=_________,y=___________.(不必证明)
★●运用 在图2中,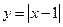 的图象x轴交于P点。一次函数
的图象x轴交于P点。一次函数 与
与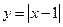 的图象交点为A,B.
的图象交点为A,B.
① 求出交点A
求出交点A ,B的坐标(用k表示);
,B的坐标(用k表示);
②若D为AB中点,且PD垂直于AB时,请利用上面的结论求出k的值。

课题学习(本题10分)
●探究 (1) 在图1中,已知线段AB,CD,其中点分别为E,F.
①若A (-1,0), B (3,0),则E点坐标为__________;
②若C (-2,2), D (-2,-1),则F点坐标为__________;
(2)在图2中,已知线段AB的端点坐标为A(a,b) ,B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程.
●归纳 无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d), AB中点为D(x,y) 时,x=_________,y=___________.(不必证明)
★●运用
在图2中, 的图象x轴交于P点。一次函数
的图象x轴交于P点。一次函数 与
与 的图象交点为A,B.
的图象交点为A,B.
①求出交点A,B的坐标(用k表示);
②若D为AB中点,且PD垂直于AB时,请利用上面的结论求出k的值。


 x,y) 时,x=_________,y=___________.(不必证明)
x,y) 时,x=_________,y=___________.(不必证明)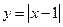 的图象x轴交于P点。一次函数
的图象x轴交于P点。一次函数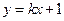 与
与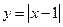 的图象交点为A,B.
的图象交点为A,B. 求出交点A
求出交点A ,B的坐标(用k表示);
,B的坐标(用k表示);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com