(本题满分12分)学完二次函数后，同学们对二次函数的图象抛物线产生了浓厚兴趣，在一次数学实验课上，孔明同学用一把宽3 cm且带刻度的矩形直尺对抛物线进行了如下测量：

 　 ①量得OA＝3 cm；

  　②把直尺的左边与抛物线的对称轴重合，使得直尺左下端点与抛物线的顶点重合(如图①)，测得抛物线与直尺右边的交点C的刻度读数为4.5．

  　请完成下列问题：

 　 1.(1)求抛物线的对称轴．

 　 2.(2)求抛物线所对应的函数关系式．

  　3.(3)将图中的直尺(足够长)沿水平方向向右平移到点A的右边(如图②)，直尺的两边交x轴于点H、G，交抛物线于点E、F．求证：S梯形EFGH＝(EF²－9)．

(本题满分12分)学完二次函数后，同学们对二次函数的图象抛物线产生了浓厚兴趣，在一次数学实验课上，孔明同学用一把宽3 cm且带刻度的矩形直尺对抛物线进行了如下测量：

 　 ①量得OA＝3 cm；

  　②把直尺的左边与抛物线的对称轴重合，使得直尺左下端点与抛物线的顶点重合(如图①)，测得抛物线与直尺右边的交点C的刻度读数为4.5．

  　请完成下列问题：

 　 1.(1)求抛物线的对称轴．

 　 2.(2)求抛物线所对应的函数关系式．

  　3.(3)将图中的直尺(足够长)沿水平方向向右平移到点A的右边(如图②)，直尺的两边交x轴于点H、G，交抛物线于点E、F．求证：S梯形EFGH＝(EF²－9)．

已知：如图，矩形ABCD中，CD＝2，AD＝3，以C点为圆心，作一个动圆，与线段AD交于点P（P和A、D不重合），过P作⊙C的切线交线段AB于F点.
（1）求证：△CDP∽△PAF；
（2）设DP＝x，AF＝y，求y关于x的函数关系式，及自变量x的取值范围；
（3）是否存在这样的点P，使△APF沿PF翻折后，点A落在BC上，请说明理由.（本题12分）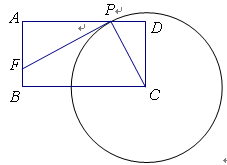

（本题12分）已知二次函数的图象经过点（0，-3），且顶点坐标为（-1，-4）.
（1）求该二次函数的解析式；
（2）设该二次函数的图象与x轴的交点为A、B，与y轴的交点为C，求△ABC的面积.

（本题12分）

如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如：，，，因此，，这三个数都是神秘数．

（1）和这两个数是神秘数吗？为什么？

（2）设两个连续偶数为和（其中取非负整数），由这两个连续偶数构造的神秘数是的倍数吗？为什么？

（3）两个连续奇数的平方差（取正数）是神秘数吗？为什么？