
题目列表(包括答案和解析)
(本题10分)在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B(8,0),斜边AO=10,C为AO的中点,反比例函数 的图象经过点C,且与AB交于点D。
的图象经过点C,且与AB交于点D。

(1)求此反比例函数的解析式;
(2)求线段AD的长度。
(本题10分)
在向红星镇居民介绍王家庄位置的时候,我们可以这样说:如图,在以红星镇为原点,正东方向为x轴正方向,正北方向为y轴正方向的平面直角坐标系(1单位长度表示的实际距离为1km)中,王家庄的坐标为(5,5);也可以说,王家庄在红星镇东北方向 km的地方。
km的地方。
还有一种方法广泛应用于航海、航空、气象、军事等领域。如右下图:在红星镇所建的雷达站O的雷达显示屏上,把周角每15°分成一份,正东方向为0°,相邻两圆之间的距离为1个单位长度(1单位长度表示的实际距离为1km),现发现2个目标,我们约定用(10,15°)表示点M在雷达显示器上的坐标,则:
(1)点N可表示为 ;王家庄位置可表示为 ;点N关于雷达站点0成中心对称的点P的坐标为 ;
(2)S△OMP= ;
(3)若有一家大型超市A在图中(4,30°)的地方,请直接标出点A,并将超市A与雷达站O连接,现准备在雷达站周围建立便民服务店B,使得△ABO为底角30°的等腰三角形,请直接写出B点在雷达显示屏上的坐标.
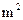 和乙种板材18000
和乙种板材18000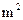 的任务.
的任务.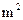 或乙种板材20
或乙种板材20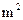 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务? 两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间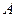 型板房和一间
型板房和一间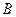 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
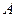 型板房 型板房 | 54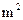 | 26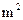 | 6 |
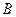 型板房 型板房 | 78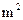 | 41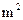 | 9 |
(本题10分)在灾民安置工作中,某企业接到一批生产甲种板材36000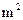 和乙种板材18000
和乙种板材18000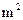 的任务.
的任务.
(1)已知该企业安排210人 生产这两种板材,每人每天能生产甲种板材30
生产这两种板材,每人每天能生产甲种板材30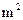 或乙种板材20
或乙种板材20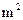 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建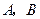 两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间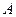 型板
型板 房和一间
房和一间 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
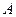 型板房 型板房 | 54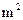 | 26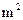 | 6 |
 型板房 型板房 | 78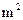 | 41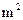 | 9 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com