
题目列表(包括答案和解析)
| 1 |
| 4 |
| A、5 | ||
B、
| ||
| C、4 | ||
| D、17-4π |
如图1至图5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c. 阅读理解:
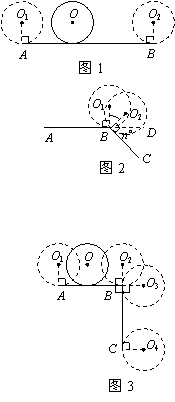
(1)如图1,⊙O从⊙O1的位置出发,沿AB滚 动到⊙O2的位置,当AB = c时,⊙O恰好自转1周.
(2)如图2,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋转的角∠O1BO2 = n°,⊙O在点B处自转![]() 周.
周.
实践应用:
(1)在阅读理解的(1)中,若AB = 2c,则⊙O自转 周;若AB = l,则⊙O自转 周.在阅读理解的(2)中,若∠ABC = 120°,则⊙O在点B处自转 周;若∠ABC = 60°,则⊙在点B处自转 周.
(2)如图3,∠ABC=90°,AB=BC=![]() c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.
c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.
拓展联想:
(1)如图4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
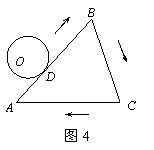
(2)如图5,多边形的周长为l,⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.
 | |
可能性大小的探计和应用
如图所示的转盘被分成了面积相等的10个数字区域,转动转盘,转到哪一个数都是一个不确定事件,由于这10个数字区域的面积相等,因而转到每一个数字的可能性是一样的,所以转到每一个数字都有![]() 的可能性,故转动转盘一次转到9的可能性只有
的可能性,故转动转盘一次转到9的可能性只有![]() .
.
将数字区域“0”、“1”作为区域A,数字区域“2”、“3”作为区域B,数字区域“4”、“5”作为区域C,数字区域“6”、“7”作为区域D,数字区域“8”、“9”作为区域E,这样整个转盘被分成了面积相等的五部分,转动转盘,指针落在这五大区域的可能性是一样的,也就是说指针落在区域A、B、C、D、E的可能性都只占![]() ,故转动转盘一次,转出的数字是8或9的可能性占
,故转动转盘一次,转出的数字是8或9的可能性占![]() ,转出数字是6或7的可能性也为
,转出数字是6或7的可能性也为![]() ,进一步推想转动转盘一次,转出是3或8的可能性占
,进一步推想转动转盘一次,转出是3或8的可能性占![]() .
.
依此类推,转动转盘一次,指针落在大于6的数字区域的可能性占![]() ;转动转盘一次,指针落在大于5的数字区域的可能性占
;转动转盘一次,指针落在大于5的数字区域的可能性占![]() ……,转动转盘一次,指针落在这些区域的可能性的大小正好等于这些区域的面积占整个转盘的面积之比.
……,转动转盘一次,指针落在这些区域的可能性的大小正好等于这些区域的面积占整个转盘的面积之比.
一般地,如果一个区域的面积为m,整个转盘的面积为n,那么转动转盘一次,指针落在这一区域的可能性为![]() .
.
由转盘可以推广到生活中的其他情况.如一个袋中有n个大小形状相同的球,只有颜色的区别,如果其中有m个红球,那么从中任意摸取一个,取得红球的可能性为![]() .应用这样的规律,我们可以解决许多生活中的实际问题.
.应用这样的规律,我们可以解决许多生活中的实际问题.
连续转动上述转盘两次,都转到数字“9”的可能性为多少?连续转动转盘四次,转到数字“1”“0”“0”“0”可能吗?可能性有多大?
 2、已知,如图,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE、MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( )
2、已知,如图,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE、MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( )| 7 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com