题目列表(包括答案和解析)
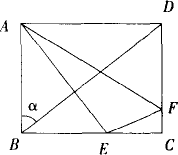
如下图，在矩形ABCD中，BD＝20，AD＞AB，设∠ABD＝
，已知sin是方程25x2－35x＋12＝0的一个实根，点E、F分别是BC、DC上的点，EC＋CF＝8，设BE＝x，△AEF的面积等于y．问BE为何值时，△AEF的面积最小？最小面积是多少？
在四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的一点，且
＝k(k＞0)．
阅读下列材料，然后回答后面的问题：
连接BD，∵
∴EH∥BD．
又∵
，∴FG∥BD，
∴FG∥EH．
(1)连接AC，则EF与GH是否一定平行．答：________．
(2)当k值为________时，四边形EFGH为平行四边形．
(3)在(2)的情形下，对角线AC与BD只需满足________条件时，EFGH为矩形．
(4)在(2)的情形下，对角线AC与BD只需满足________条件时，EFGH为菱形．
如图，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：
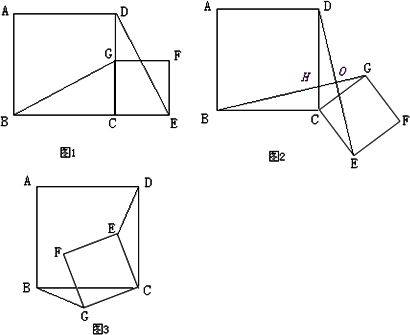
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判
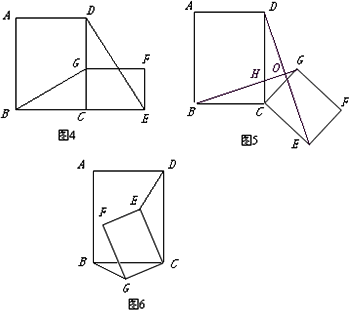
(2)将原题中正方形改为矩形(如图图6)，且AB＝a，BC＝b，CE＝ka，CG＝kb(a≠b，k＞0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．
(3)在第(2)题图5中，连结DG、BE，且a＝3，b＝2，k＝
，求BE2＋DG2的值．
如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断．
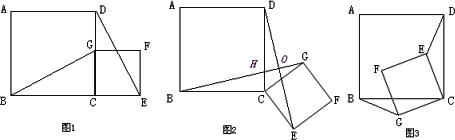
(2)将原题中正方形改为矩形(如图4－6)，且AB＝a，BC＝b，CE＝ka，CG＝kb(a≠b，k＞0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．
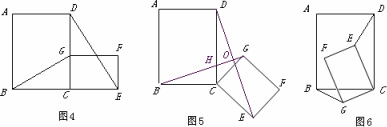
(3)在第(2)题图5中，连结DG、BE，且a＝3，b＝2，k＝
，求BE2＋DG2的值．
（1）如图①，P为△ABC的边AB上一点（P不与点A、点B重合），连接PC，如果△CBP∽△ABC，那么就称P为△ABC的边AB上的相似点．
画法初探
①如图②，在△ABC中，∠ACB＞90°，画出△ABC的边AB上的相似点P（画图工具不限，保留画图痕迹或有必要的说明）；
辩证思考
②是不是所有的三角形都存在它的边上的相似点？如果是，请说明理由；如果不是，请找出一个不存在边上相似点的三角形；
特例分析
③已知P为△ABC的边AB上的相似点，连接PC，若△ACP∽△ABC，则△ABC的形状是 ；
④如图③，在△ABC中，AB＝AC，∠A＝36°，P是边AB上的相似点，求的值．
（2）在矩形ABCD中，AB＝a，BC＝b（a≥b）．P是AB上的点（P不与点A、点B重合），作PQ⊥CD，垂足为Q．如果矩形ADQP∽矩形ABCD，那么就称PQ为矩形ABCD的边AB、CD上的相似线．
①类比（1）中的“画法初探”，可以提出问题：对于如图④的矩形ABCD，在不限制画图工具的前提下，如何画出它的边AB、CD上的相似线PQ呢？
你的解答是： （只需描述PQ的画法，不需在图上画出PQ）．
②请继续类比（1）中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究，要求每个栏目提出一个问题并解决．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com