
题目列表(包括答案和解析)
| x+4 |
| 3 |
| 2x-7 |
| 4 |
| 5 |
| 2 |
 (a>0).
(a>0). 上,请说明理由.
上,请说明理由.已知一抛物线经过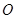 (0,0),
(0,0), (1,1)两点,且解析式的二次项系数为
(1,1)两点,且解析式的二次项系数为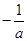
( >0).
>0).
【小题1】当 时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
【小题2】已知点 (0,1),若抛物线与射线
(0,1),若抛物线与射线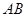 相交于点
相交于点 ,与
,与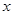 轴相交于点
轴相交于点 (异于原点),当
(异于原点),当 在什么范围内取值时,
在什么范围内取值时,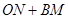 的值为常数?当
的值为常数?当 在什么范围内取值时,
在什么范围内取值时, 的值为常数?
的值为常数?
【小题3】若点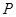 (
(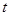 ,
,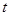 )在抛物线上,则称点
)在抛物线上,则称点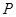 为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线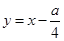 上,请说明理由.
上,请说明理由.
已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m= .
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴
翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.①请在图3
中补全小贝同学翻折后的图形;②请你根据①中的图形,求出m的取值范围,并简要说明理
由.
 (a>0).
(a>0). 上,请说明理由.
上,请说明理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com