
题目列表(包括答案和解析)
 AD交⊙A于E,EC的延长线交⊙B于F.
AD交⊙A于E,EC的延长线交⊙B于F.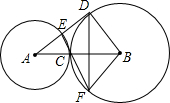 AD交⊙A于E,EC的延长线交⊙B于F.
AD交⊙A于E,EC的延长线交⊙B于F.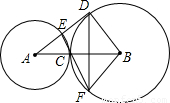


 BC。
BC。 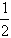 BC。
BC。 (AD+BC)吗?
(AD+BC)吗?阅读以下内容:
如图(1),在ABC中,由DE∥BC,我们可以得到△ADE∽△ABC,
从而有 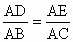 ,
,
即AD·AC=AE·AB,于是
AD·(AE+EC)=AE·(AD+DB),AD·EC=AE·DB,
从而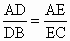 ,即△ABC中BC的平行线DE将另两条边AB、AC分割为成比例的线段.
,即△ABC中BC的平行线DE将另两条边AB、AC分割为成比例的线段.
我们已经知道,如果D是AB的中点,则E是AC的中点.
现在请你回答下列问题,并说说你的理由:
(1)如图(2),DE∥FG∥BC,AD=DF=FB,那么AE、EG、GC有什么关系?
(2)如图(3),DE∥FG∥BC,DF=FB,那么EG与GC有什么关系?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com