
题目列表(包括答案和解析)
你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积) s(mm2)的反比例函数,其图像如图所示。

1.写出y与s的函数关系式;
2.求当面条粗1.6mm2时,面条的总长度 是多少米?(考查反比例函数的应用)
你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积) s (mm2)的反比例函数,其图像如图所示。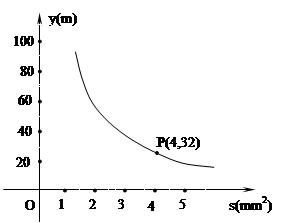
【小题1】写出y与s的函数关系式;
【小题2】求当面条粗1.6mm2时,面条的总长度 是多少米?(考查反比例函数的应用)
你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积) s (mm2)的反比例函数,其图像如图所示。

1.写出y与s的函数关系式;
2.求当面条粗1.6mm2时,面条的总长度 是多少米?(考查反比例函数的应用)
(10分)(1)探究归纳:如图,已知△ABC与△ABD的面积相等,试判断
【小题1】(1)AB与CD的位置关系,并说明理由.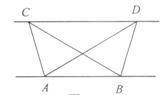
【小题2】(2)结论应用:①如图,点M,N在反比例函数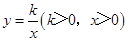 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.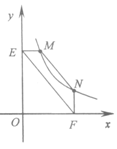
②如图,点M,N在反比例函数y=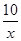 的图象上,且M(2,m),N是第三象限内反比例函数y=
的图象上,且M(2,m),N是第三象限内反比例函数y=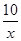 的图象上一动点.过点M作ME⊥y轴,过点N作EF⊥x轴,垂足分别为E,F.说明MN∥EF.并求当四边形MEFN的面积为12时点N的坐标.
的图象上一动点.过点M作ME⊥y轴,过点N作EF⊥x轴,垂足分别为E,F.说明MN∥EF.并求当四边形MEFN的面积为12时点N的坐标.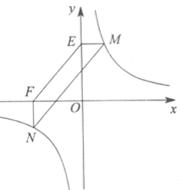
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com