图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=

n(n+1)

2

．
如果图1中的圆圈共有12层，我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是．

图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面-层有一个圆圈，以下各层均比上-层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=

n(n+1)

2

．

如果图1中的圆圈共有12层，
（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是；
（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数-23，-22，-21，…，求图4中所有圆圈中各数的绝对值之和．

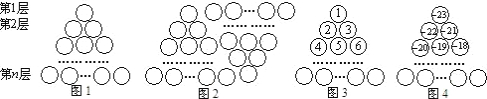
如图是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为．

 

 

 

 

　　　　　　　图１　　　　　　　　图2　　　　　　　　　图3　　　　　　　　图4

如果图1中的圆圈共有12层，（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数，则最底层最左边这个圆圈中的数是              ；（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数，，，，求图4中所有圆圈中各数的绝对值之和．

 

图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为

　　　　　　

如果图1中的圆圈共有12层，（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,，则最底层最左边这个圆圈中的数是                ；（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数-23，-22，-21，，求图4中所有圆圈中各数的绝对值之和．