（18分）请回答下列Ⅰ、Ⅱ小题
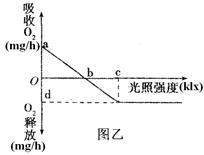
Ⅰ、（8分）图甲表示在光照充足、CO₂浓度适宜的条件下，温度对某植物真正光合作用速率和呼吸作用速率的影响。其中实线表示真正光合作用速率，虚线表示呼吸作用速率。图乙为该植物在适宜条件下，光合作用速率随光照强度变化的示意图。请据图回答：

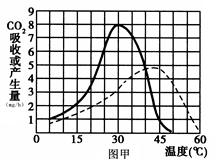
（1）由图甲可知，与             作用有关的酶对高温更为敏感。温度会影响光合作用的                          阶段。
（2）当环境温度为40℃时，该植物的有机物净积累量为        mg/h。理论上预计，在温度为        条件下，植物生长状况达到最佳，已知乙图是在此温度条件下绘制而成的曲线，理论上分析，如果温度改变为45℃，图中b点将向        移。
（3）乙图中用                                     的量表示植物的光合作用速率，图中c点表示                                 
（4）乙图曲线中，当光照强度为0时，叶肉细胞中产生ATP的细胞器有              。
Ⅱ、（10分）大麻是一种雌雄异株的植物，请回答以下问题：

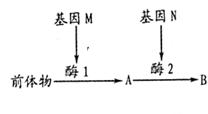
（1）在大麻体内，物质B的形成过程如右图所示，基因Mm和Nn分别位于两对常染色体上。
①据图分析，能产生B物质的大麻基因型可能有           种。
②如果两个不能产生B物质的大麻品种杂交，F₁全都能产生B物质，则亲本的基因
型是                  和                 。F₁中雌雄个体随机相交，后代中
能产生B物质的个体数和不能产生B物质的个体数之比应为              。
（2）右图为大麻的性染色体示意图，X、Y染色体的同源部分（图中I片断）上的基因互为等位，非同源部分（图中Ⅱ₁、Ⅱ₂片断）上的基因不互为等位。若大麻的抗病性状受性染色体上的显性基因D控制，大麻的雌、雄个体均有抗病和不抗病类型。请回答：

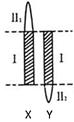
①控制大麻抗病性状的基因不可能位于右图中的        　   片段。
②请写出具有抗病性状的雄性大麻个体可能有的基因型      　　 。
③现有雌性不抗病和雄性抗病两个品种的大麻杂交，请根据以下子代可能出现的情
况，分别推断出这对基因所在的片段：
如果子代全为抗病，则这对基因位于 　   　 片段。
如果子代雌性全为不抗病，雄性全为抗病，则这对基因位于  　       片段。
如果子代雌性全为抗病，雄性全为不抗病，则这对基因位于     　           片
段。

探索问题：（1）比较下列数的大小：

2

3

3

4

，

5

13

9

17

，

14

23

19

28

．
（2）根据上述规律，可以得出下面的结论：一个真分数

a

b

（a、b均为正数），给其分子、分母同加上一个正数m，得

a+m

b+m

，则这两个分数的大小关系是：

a

b

a+m

b+m

．
（3）请你用文字叙述（2）中的结论：；
（4）请你用图形的面积说明（2）中结论的正确性．
（5）请你用已学的其他数学知识说明（2）中结论的正确性．
（6）这个结论可以解释生活中的许多现象，解决生活中许多与数学有关的问题．请你再提出一个类似的数学问题，或举出一个生活中与此结论相关的例子．