
题目列表(包括答案和解析)
 (2013•丰台区二模)操作探究:
(2013•丰台区二模)操作探究: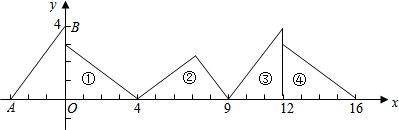
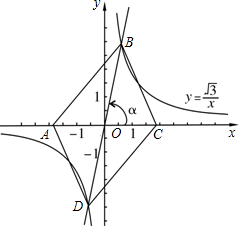 我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数y=
我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数y=
| ||
| x |
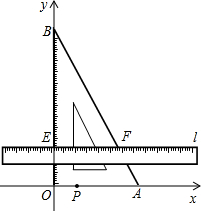 阅读材料:在直角三角形中,30°所对的直角边是斜边的一半.
阅读材料:在直角三角形中,30°所对的直角边是斜边的一半.| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 9 |
| 2 |
| 9 |
| 2 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com