
题目列表(包括答案和解析)
| 3×4 | 2 |

 =6条直线.请你仿照上面分析方法,回答下面问题:
=6条直线.请你仿照上面分析方法,回答下面问题:
(1)若平面上有五个点A、B、C、D、E,其中任何三点都不在一条直线上,过每两点画一条直线,一共可以画出_条直线.
若平面上有符合上述条件的六个点,一共可以画出_条直线;
若平面上有符合上述条件的n个点,一共可以画出_条直线(用含n的式子表示).
(2)若我校初中24个班之间进行篮球比赛,第一阶段采用单循环比赛(每两个班之间比赛一场),类比上面的分析计算第一阶段比赛的总场次是多少?
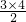 =6条直线.请你仿照上面分析方法,回答下面问题:
=6条直线.请你仿照上面分析方法,回答下面问题:
列一元二次方程解应用题的关键是审题,要善于理解题意,分析题目中的________关系,可采用________、________等分析方法,恰当地设出________,准确地找出已知量与________之间的关系,正确地列出________,求得问题的正确答案.同时要注意根据具体问题的实际意义检验结果的________.其步骤有下面的六步:(1)审题;(2)________;(3)________;(4)________;(5)________;(6)________.
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com