
题目列表(包括答案和解析)
某商店以每件42元的价格购进一种服装,根据试销得知:这种服装每天的销售量t件与每件的销售价x元可看成一次函数关系:t=-3x+204.
(1)写出商店卖这种服装每天的销售利润y与每件的销售价x元之间的函数关系式;
(2)通过对所得函数关系式进行配方,说出商店要想每天获得最大的销售利润,每件的销售价定为多少最为合适?最大销售利润是多少?
 (件),与每件的销售价
(件),与每件的销售价  (元/件)可看成是一次函数关系:
(元/件)可看成是一次函数关系:
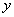 与每件的销售价
与每件的销售价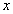 之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差); 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com