
题目列表(包括答案和解析)
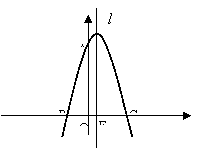
已知二次函数![]() 的图像与x轴交于B(-2,0),C(4,0)两点,点E是对称轴
的图像与x轴交于B(-2,0),C(4,0)两点,点E是对称轴![]() 与
与![]() 的交点.
的交点.
(1)求二次函数的解析表达式;
(2)T为对称轴![]() 上一动点,以点B为圆心,BT为半径作⊙B,写出直线CT与⊙B相切时,T点的坐标;
上一动点,以点B为圆心,BT为半径作⊙B,写出直线CT与⊙B相切时,T点的坐标;
(3)若在x轴上方的P点为抛物线上的动点,且∠BPC为锐角,直接写出PE的取值范围.
(4)对于(1)中得到的关系式,若![]() 为整数,在使得
为整数,在使得![]() 为完全平方数的所有
为完全平方数的所有![]() 的值中,设
的值中,设![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,次小值为
,次小值为![]() ,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数.)求
,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数.)求![]() 的值.
的值.
 | |||
| |||
已知二次函数![]() 的图像与x轴交于B(-2,0),C(4,0)两点,点E是对称轴
的图像与x轴交于B(-2,0),C(4,0)两点,点E是对称轴![]() 与
与![]() 的交点.
的交点.
(1)求二次函数的解析表达式;
(2)T为对称轴![]() 上一动点,以点B为圆心,BT为半径作⊙B,写出直线CT与⊙B相切时,T点的坐标;
上一动点,以点B为圆心,BT为半径作⊙B,写出直线CT与⊙B相切时,T点的坐标;
(3)若在x轴上方的P点为抛物线上的动点,且∠BPC为锐角,直接写出PE的取值范围.
(4)对于(1)中得到的关系式,若![]() 为整数,在使得
为整数,在使得![]() 为完全平方数的所有
为完全平方数的所有![]() 的值中,设
的值中,设![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,次小值为
,次小值为![]() ,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数.)求
,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数.)求![]() 的值.
的值.
 | |||
| |||
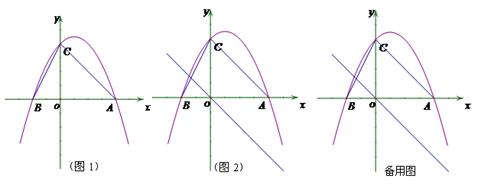
如图1,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A、点B,与y轴交于点C,且A、B两点的坐标分别是(4,0)、(0,-2),tan∠BCO=![]() (1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
(1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
【解析】(1)利用A、B两点的坐标和tan∠BCO=![]() 求抛物线解析式
求抛物线解析式
(2)设点m(x,y),则由以MB为直径的圆与直线BC相切于点B,说明了点B为直径的一个端点,另外,BC直线方程为y=2x+4,利用BM的中点就是圆心坐标,BM垂直于CB,因此联立方程组可得M的坐标
(3)假设存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形
则有几种情况的一种直角为C,直角为P,直角为O,直角为Q的情况,那么分情况讨论求解,利用一组对边平行,一个角为直角,进行求解
如图1,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A、点B,与y轴交于点C,且A、B两点的坐标分别是(4,0)、(0,-2),tan∠BCO=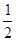 (1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
(1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
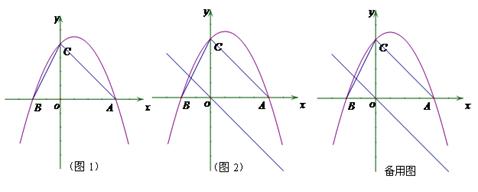
【解析】(1)利用A、B两点的坐标和tan∠BCO=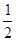 求抛物线解析式
求抛物线解析式
(2)设点m(x,y),则由以MB为直径的圆与直线BC相切于点B,说明了点B为直径的一个端点,另外,BC直线方程为y=2x+4,利用BM的中点就是圆心坐标,BM垂直于CB,因此联立方程组可得M的坐标
(3)假设存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形
则有几种情况的一种直角为C,直角为P,直角为O,直角为Q的情况 ,那么分情况讨论求解,利用一组对边平行,一个角为直角,进行求解
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com