
题目列表(包括答案和解析)
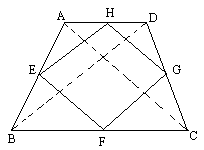
我们把任一四边形四边的中点依次连接成的四边形叫做中点四边形.(1)这个中点四边形有什么特征?请证明你的结论;(2)若要使这个中点四边形是矩形,则原四边形至少要具备的一个条件是什么?(3)若要使这个中点四边形是菱形,则原四边形至少要具备的一个条件又是什么?以上写出条件即可,不必证明.
已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF。
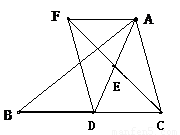
(1)求证:AF=DC;
(2)若AD=CF,试判断四边形AFDC是什么样的四边形?并证明你的结论。
【解析】(1)因为AF∥DC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,故有AF=DC;
(2)由(1)知,AF=DC且AF∥DC,可得四边形AFDC是平行四边形,又因为AD=CF,故可根据对角线相等的平行四边形是矩形进行判定.
 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
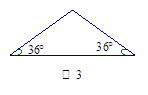
数学课上,同学们探究发现:如图1,顶角为36°的等腰三角形具有一种特性,即经过它某一顶点的一条直线可把它分成两个小等腰三角形. 并且对其进行了证明.
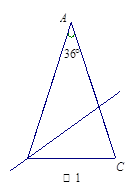
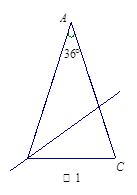
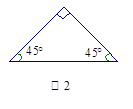
1.证明后,小乔又发现:下面两个等腰三角形如图2、图3也具有这种特性.请你在
图2、图3中分别画出一条直线,把它们分成两个小等腰三角形,并在图中标出所画等腰三角形两个底角的度数;
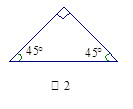
2.接着,小乔又发现:直角三角形和一些非等腰三角形也具有这样的特性,如:直角三角形斜边上的中线可以把它分成两个小等腰三角形.请你画出一个具有这种特性的三角形的示意图,并在图中标出此三角形的各内角的度数.(说明:要求画出的既不是等腰三角形,也不是直角三角形.)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com