(本小题满分8分)

   某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠围墙(墙的长度不限)，另三边用木栏围成，建成的苗圃为如图所示的长方形ABCD。已知木栏总长为120米，设AB边的长为x米，长方形ABCD的面积为S平方米．

   1.(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)．当x为何值时，S取得最值(请指出是最大值还是最小值)?并求出这个最值；

   2.(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆，其圆心分别为和，且到AB、BC、AD的距离与到CD、BC、AD的距离都相等，并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面，以方便同学们参观学习．当(l)中S取得最值时，请问这个设计是否可行?若可行，求出圆的半径；若不可行，清说明理由．

(本小题满分8分)

某单位准备印制一批证书．现有两个印刷厂可供选择．甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷教量收取印刷费．甲、乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示．

1.（1）请你直接写出甲厂的制版费及与x的函数解析式．并求出其证书印刷单价．

2.（2）当印制证书8千个时．应选择哪个印刷厂节省费用．节省费用多少元?

3.（3）如果甲厂想把8千个证书的印制工作承揽下来，在不降低制版费的前提下，每个证书最少降低多少元?

(本小题满分14分)平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别为(0，3)、(，0)，将此平行四边形绕点0顺时针旋转90°，得到平行四边形。

(1)若抛物线过点C，A，，求此抛物线的解析式；

(2)求平行四边形ABOC和平行四边形重叠部分△的周长；

(3)点M是第一象限内抛物线上的一动点，间：点M在何处时△的面积最大?最大面积是多少?并求出此时点M的坐标。

(本小题满分8分)

如图，在梯形ABCD中，DC∥AB，AD=BC， BD平分∠ABC，∠A=60°，过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF，求证：△DEF为等边三角形。

(本小题满分9分)

如图所示，抛物线与x轴交于A、B两点，直线BD的函数表达式为，抛物线的对称轴l与直线BD交于点C、与x轴交于点E．

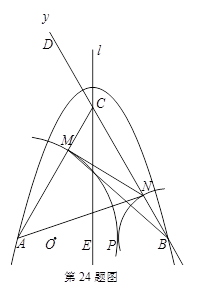
⑴求A、B、C三个点的坐标．

⑵点P为线段AB上的一个动点（与点A、点B不重合），以点A为圆心、以AP为半径的圆弧与线段AC交于点M，以点B为圆心、以BP为半径的圆弧与线段BC交于点N，分别连接AN、BM、MN．

①求证：AN=BM．

②在点P运动的过程中，四边形AMNB的面积有最大值还是有最小值？并求出该最大值或最小值.