例4 如图5.在⊙O中.AB.AC是互相垂直的两条弦. AB＝8cm.AC＝6cm.那么⊙O的半径OA的长( ) A．4 cm B．5 cm C．6 cm D．8 cm [分析]要求半——青夏教育精英家教网—

例4 如图5.在⊙O中.AB.AC是互相垂直的两条弦. AB＝8cm.AC＝6cm.那么⊙O的半径OA的长( ) A．4 cm B．5 cm C．6 cm D．8 cm [分析]要求半径OA的长.可通过垂径定理构造Rt△.于是过O分别作OD⊥AB.OE⊥AC.则可得矩形ADOE. 解:如图5.过O分别作OD⊥AB于D.OE⊥AC于E. 则得矩形ADOE.∴ OD＝AE. 又∵ AD＝AB＝4.OD＝AE＝AC＝3, ∴ AO＝＝5cm．故选(B)．本资料由提供! 【查看更多】

我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）ⁿ（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）²=a²+2ab+b²展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）³=a³+3a²b+3ab²+b²展开式中的系数等等．

（1）根据上面的规律，则（a+b）⁵的展开式=

a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵

．
（2）利用上面的规律计算：2⁵-5×2⁴+10×2³-10×2²+5×2-1=

1

．

查看答案和解析>>

我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）ⁿ（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）²=a²+2ab+b²展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）³=a³+3a²b+3ab²+b³展开式中的系数等等．

（1）根据上面的规律，写出（a+b）⁵的展开式．
（2）利用上面的规律计算：3⁵-5×3⁴+10×3³-10×3²+5×3-1．

查看答案和解析>>

如图（1），四边形ABCD内部有一点P，使得S_△APD+S_△BPC=S_△PAB+S_△PCD，那么这样的点P叫做四边形ABCD的等积点．
（1）如果四边形ABCD内部所有的点都是等积点，那么这样的四边形叫做等积四边形．
①请写出你知道的等积四边形：

，

，（四例）
②如图（2），若四边形ABCD是平行四边形且S_△ABP=8，S_△APD=7，S_△BPC=15，则S_△PCD=

．
（2）如图（3），等腰梯形ABCD，AD=4，BC=10，AB=5，直线l为等腰梯形的对称轴，分别交AD于点E，交BC于点F．
①请在直线l上找到等腰梯形的等积点，并求出PE的长度．
②请找出等腰梯形ABCD内部所有的等积点，并画图表示．

查看答案和解析>>

19、我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）ⁿ（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）²=a²+2ab+b²展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）³=a³+3a²b+3ab²+b²展开式中的系数等等．

（1）根据上面的规律，写出（a+b）⁵的展开式．
（2）利用上面的规律计算：2⁵-5×2⁴+10×2³-10×2²+5×2-1．

查看答案和解析>>

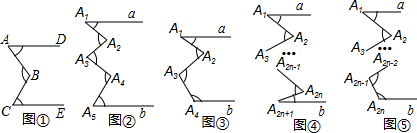
（1）引例：如图①所示，直线AD∥CE．求证：∠B=∠A+∠C．
（2）变式：如图②所示，a∥b，请判断∠A₁、∠A₂、∠A₃、∠A₄、∠A₅之间的大小关系，直接写出结论，无需证明．
答：

∠A₁+∠A₃+∠A₅=∠A₂+∠A₄

．
如图③a∥b，请判断∠A₁、∠A₂、∠A₃、∠A₄之间的大小关系，直接写出结论，无需证明．
（3）推广：如图④a∥b，请判断∠A₁、∠A₂、∠A₃、…、∠A_2n之间的大小关系，直接写出结论，无需证明（注意图中的“…”）
答：

∠A₁+∠A₃+…+∠A_2n+1=∠A₂+∠A₄+…+∠A_2n

．
如图⑤，a∥b，请判断∠A₁、∠A₂、∠A₃、…、∠A_2n+1之间的大小关系，直接写出结论，无需证明（注意图中的“…”）
答：

∠A₁+∠A₃+…+∠A_2n+1=∠A₂+∠A₄+…+∠A_2n-2+180°-∠A_2n

．

查看答案和解析>>

练习册

高中

初中

小学