
题目列表(包括答案和解析)
| 2 |
| 2 |
| 3 |
| 3 |
| 12 |
| 3 |
| ||
|
| ||||
|
| ||
| 3 |
| 1 | ||
|
1•
| ||||
|
1•
| ||||
|
| ||
| 6 |
| ||
| 6 |
| ||
|
| ||||
|
| ||||
|
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 6 |
| 2 |
| 6 |
| 2 |
| 7 |
| 7 |
| 7 |
| 1 | ||
|
 •
• =______;
=______; •
• =______;
=______; •
• =______;显然将一个二次根式乘以一个适当的二次根式后结果不再含有根号.因此利用这个性质结合二次根式除法法则、分式基本性质可以化去分母中的根号,使分母中不再含有根号,如:
=______;显然将一个二次根式乘以一个适当的二次根式后结果不再含有根号.因此利用这个性质结合二次根式除法法则、分式基本性质可以化去分母中的根号,使分母中不再含有根号,如: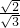 =
=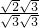 =
= .
.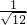 =______=______;②
=______=______;②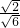 =______=______;
=______=______; )(2-
)(2- )=______;(
)=______;( ﹢
﹢ )(
)( -
- )=______;同样发现相乘的积不再含有根号.想一想:(
)=______;同样发现相乘的积不再含有根号.想一想:( -3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简:
-3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简: .
.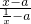 有意义的x应满足的条件是
有意义的x应满足的条件是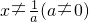
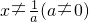
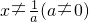
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com