
题目列表(包括答案和解析)
如图,已知△ABC中,∠B=48°,∠C=62°,点E、点F分别在边AB和边AC上,将把△AEF沿EF折叠得△DEF,点D正好落在边BC上(点D不与点B.点C重合).
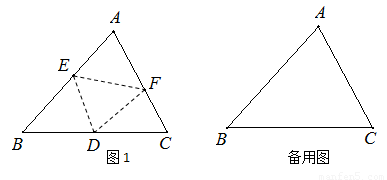
(1)如图1,若BD=BE,则△CDF是否为等腰三角形?请说明理由.
(2)△BDE、△CDF能否同时为等腰三角形?若能,请画出所有可能的图形,并直接指出△BDE、△CDF的三个内角度数;若不能,请说明理由.

 AB·h1+
AB·h1+ AC·h2=
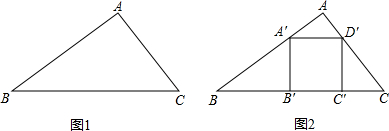
AC·h2= BC·h,可得h1+h2=h,又因为h3=0,所以:h1+h2+h3=h。图②~⑤中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外。
BC·h,可得h1+h2=h,又因为h3=0,所以:h1+h2+h3=h。图②~⑤中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外。
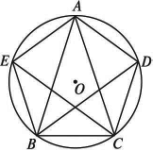
如图,已知圆O的内接等腰三角形ABC,AB=AC,弦BD、CE分别平分∠ABC、∠ACB,BE=BC.求证:五边形AEBCD是正五边形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com