
题目列表(包括答案和解析)
解:(1)由题意知,当![]() 、
、![]() 运动到
运动到![]() 秒时,如图①,过
秒时,如图①,过![]() 作
作![]() 交
交![]() 于
于![]() 点,则四边形
点,则四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴ ![]() .解得
.解得![]() . 5分
. 5分
(2)分三种情况讨论:
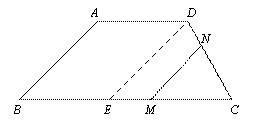
① 当![]() 时,如图②作
时,如图②作![]() 交
交![]() 于
于![]() ,则有
,则有![]() 即.
即.
 ∵
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() . 6分
. 6分
② 当![]() 时,如图③,过
时,如图③,过![]() 作
作![]() 于H.
于H.
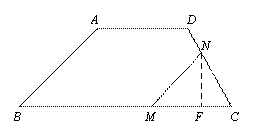 则
则![]() ,
,
∴![]() .
.
∴![]() .7分
.7分
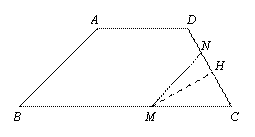
③ 当![]() 时,如图④.
时,如图④.
则![]() .
.
![]() . -------------------------------------8分
. -------------------------------------8分
综上所述,当![]() 、
、![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
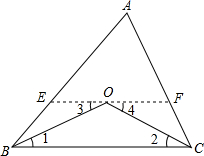 如图,已知:∠ABC=50°,∠ACB=60°,BO、CO分别是∠ABC和∠ACB的平分线.求∠BOC.
如图,已知:∠ABC=50°,∠ACB=60°,BO、CO分别是∠ABC和∠ACB的平分线.求∠BOC.| 1 | 2 |
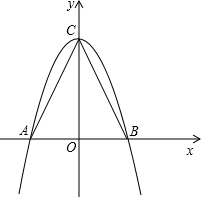 (2012•柳州)如图,在△ABC中,AB=2,AC=BC=
(2012•柳州)如图,在△ABC中,AB=2,AC=BC=| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| x2-2 |
| x2-2 |
(本题满分8分)如图1,已知反比例函数y= 过点P, P点的坐标为(3-m,
过点P, P点的坐标为(3-m,
2m),m是分式方程 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.

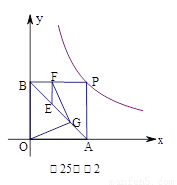
(1)求m值
(2)试判断四边形PAOB的形状,并说明理由.
(2)如图2,连结AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连结OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.
(本题12分)数学课上,李老师出示了如下框中的题目.
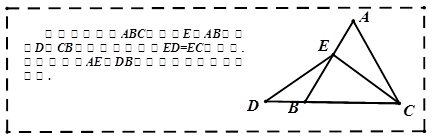
小敏与同桌小聪讨论后,进行了如下解答:
1.(1)特殊情况,探索结论
当点![]() 为
为![]() 的中点时,如图1,确定线段
的中点时,如图1,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
![]()
 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).

|
|
2.(2)特例启发,解答题目
解:题目中,![]() 与
与![]() 的大小关系是:
的大小关系是:![]()
![]() (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(请你完成以下解答过程)
3.(3)拓展结论,设计新题
在等边三角形![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() 的边长为1,
的边长为1,![]() ,求
,求![]() 的长(请你直接写出结果).
的长(请你直接写出结果).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com