
题目列表(包括答案和解析)
我们已经学过用方差来描述一组数据的离散程度,其实我们还可以用“平均差”来描述一组数据的离散程度。在一组数据x1,x2,…,xn中,各数据与它们的平均数 的差的绝对值的平均数,即T=
的差的绝对值的平均数,即T= (|x1-
(|x1- |+|x2-
|+|x2- |+…+|xn-
|+…+|xn- |)叫做这组数据的“平均差”,“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大。
|)叫做这组数据的“平均差”,“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大。
请你解决下列问题:
【小题1】分别计算下列甲乙两个样本数据的“平均差”,并根据计算结果判断哪个样本波动较大。
甲:12,13,11,10,14, 乙:10,17,10,13,10
【小题2】分别计算甲、乙两个样本数据的方差和标准差,并根据计算结果判断哪个样本波动较大.
【小题3】以上的两种方法判断的结果是否一致?
我们已经学过用方差来描述一组数据的离散程度,其实我们还可以用“平均差”来描述一组数据的离散程度。在一组数据x1,x2,…,xn中,各数据与它们的平均数 的差的绝对值的平均数,即T=
的差的绝对值的平均数,即T= (|x1-
(|x1- |+|x2-
|+|x2- |+…+|xn-
|+…+|xn- |)叫做这组数据的“平均差”,“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大。
|)叫做这组数据的“平均差”,“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大。
请你解决下列问题:
1.分别计算下列甲乙两个样本数据的“平均差”,并根据计算结果判断哪个样本波动较大。
甲:12,13,11,10,14, 乙:10,17,10,13,10
2.分别计算甲、乙两个样本数据的方差和标准差,并根据计算结果判断哪个样本波动较大.
3.以上的两种方法判断的结果是否一致?


阅读:我们知道,在数轴x=1表示一个点,而在平面直角坐标系中x=1表示一条直线;我们还知道,以二元一次方程2 x – y + 1 = 0的所有解为坐标的点组成的图形就是一次函数y=2x-1的图象,它也是一条直线如图①。
观察图①可以解出,直线x=1现直线y = 2 x -1的交点P的坐标(1,3),就是方程组![]() 的解,所以这个方程组的解为
的解,所以这个方程组的解为 ![]()

 在直角坐标系中,x≤1表示一个平面区域,即直线x = 1以及它左侧的部分,如图②;y≤2 x + 1也表示一个平面区域,即直线y = 2 x+1以及它下方的部分,如图③。
在直角坐标系中,x≤1表示一个平面区域,即直线x = 1以及它左侧的部分,如图②;y≤2 x + 1也表示一个平面区域,即直线y = 2 x+1以及它下方的部分,如图③。


(1,3)
O 1 x 1
(图①) (图②) (图③)
回答下列问题:
(1)在直角坐标系(图④)中,用作图象的方法求出方程组![]() 的解;
的解;
(2)用阴影表示  所围成的区域。
所围成的区域。

某校积极开展每天锻炼1小时活动,老师对本校八年级学生进行一分钟跳绳测试,并对跳绳次数进行统计,绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中,组中值为150次一组的 频率为0.2.(说明: 组中值为190次的组别为 180≤次数<200)
请结合统计图完成下列问题: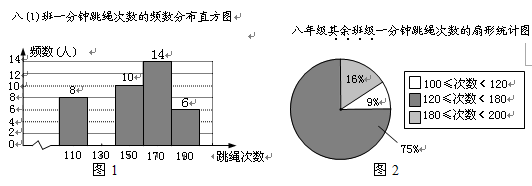
(1)八(1)班的人数是 ,组中值为110次一组的频率为 ;
(2)请把频数分布直方图补充完整;
(3)如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%,那么八年级同学至少有多少人?请写出解答过程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com