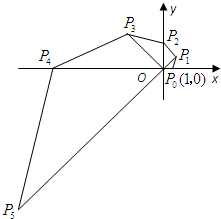如图，在直角坐标系中，已知点P₀的坐标为（1，0），将线段OP₀按逆时针方向旋转45°，将其长度伸长为OP₀的2倍，得到线段OP₁；再将线段OP₁按逆时针方向旋转45°，长度伸长为OP₁的2倍，得到线段OP₂；如此下去，得到线段OP₃，OP₄，…，OP_n（n为正整数）
（1）求点P₆的坐标；
（2）求△P₅OP₆的面积；
（3）我们规定：把点P_n（x_n，y_n）（n=0，1，2，3，…）的横坐标x_n、纵坐标y_n都取绝对值后得到的新坐标（|x_n|，|y_n|）称之为点P_n的“绝对坐标”．根据图中点P_n的分布规律，请你猜想点P_n的“绝对坐标”，并写出来．

数学课堂上，徐老师出示一道试题：如图（十）所示，在正三角形ABC中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠ACP的平分线上一点．若∠AMN＝60°，求证：AM＝MN．
    
(1)经过思考，小明展示了一种正确的证明过程．请你将证明过程补充完整．
证明：在AB上截取EA＝MC，连结EM，得△AEM．
∵∠1＝180°－∠AMB－∠AMN，∠2＝180°－∠AMB－∠B，∠AMN＝∠B＝60°，∴∠1＝∠2．
又CN平分∠ACP，∠4＝∠ACP＝60°．∴∠MCN＝∠3＋∠4＝120°…………①
又∵BA＝BC，EA＝MC，∴BA－EA＝BC－MC，即BE＝BM．
∴△BEM为等边三角形．∴∠6＝60°．
∴∠5＝180°－∠6＝120°．………②
∴由①②得∠MCN＝∠5．
在△AEM和△MCN中，
∵________________________________
∴△AEM≌△MCN (ASA)．∴AM＝MN．
(2)若将试题中的“正三角形ABC”改为“正方形A₁B₁C₁D₁”（如图），N₁是∠D₁C₁P₁的平分线上一点，则当∠A₁M₁N₁＝90°时，结论A₁M₁＝M₁N₁．是否还成立？（直接写出答案，不需要证明）
(3)若将题中的“正三角形ABC”改为“正多边形A_nB_nC_nD_n…X_n”，请你猜想：当∠A_nM_nN_n＝   °时，结论A_nM_n＝M_nN_n仍然成立？（直接写出答案，不需要证明）

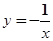将代入反比例函数中，所得的函数值记为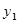，将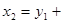1代入反比例函数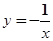中，所得的函数值记为y₂，将x₃=y₂+1代入反比例函数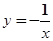中，所得的函数值记为y₃，…，将x_n=y_n-1+1代入反比例函数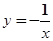中，所得的函数值记为y_n，(其中n≥2，且n是自然数)，如此继续下去.则在2006个函数值y₁，y₂，y₃，……y₂₀₀₆，中，值为2的情况共出现了         次。