
题目列表(包括答案和解析)
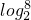 log=3(即
log=3(即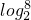 =3).
=3). 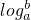 (即
(即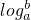 =n),如34=81,则指数4叫做以3为底81的对数,记为
=n),如34=81,则指数4叫做以3为底81的对数,记为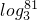 (即
(即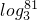 =4).
=4).将幂的运算逆向思维可以得到 ,
, ,
, ,
, ,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解,收到事半功倍的效果如:
,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解,收到事半功倍的效果如:
(1) =__________
=__________
(2) 若3×9m×27m=311,则m的值为____________.
(3) 比较大小:,则a、b、c、d的大小关系是____________
(提示:如果 ,n为正整数,那么
,n为正整数,那么 )
)
将幂的运算逆向思维可以得到 ,
, ,
, ,
, ,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解,收到事半功倍的效果如:
,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解,收到事半功倍的效果如:
(1) =__________
=__________
(2) 若3×9m×27m=311,则m的值为____________.
(3) 比较大小:,则a、b、c、d的大小关系是____________
(提示:如果 ,n为正整数,那么
,n为正整数,那么 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com