
题目列表(包括答案和解析)
| 2 |
| 13 |
| 17 |
| 2 |
| 5 |
| 26 |

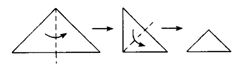
如图13所示,把腰长为1的等腰直角三角形折叠两次后,得到的一个小三角形的周长是( )
A.1+![]()
![]() B.1+
B.1+![]() C.2-
C.2-![]() D.
D.![]() -1
-1
(13) (14) (15)

| 5 |
| 10 |
| 13 |
| 5 |
| 2 |
| 17 |
| m2+16n2 |
| 9m2+4n2 |
| m2+n2 |
| a2+4 |
| b2+25 |
| a2-d2 |

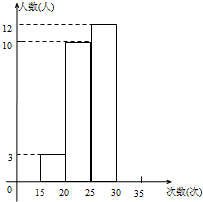 某校为了了解七年级女生的体能情况,随机抽查了部分女生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图和不完整的统计表(每个分组包括左端点,不包括右端点).请你根据图中提供的信息,解答以下问题:
某校为了了解七年级女生的体能情况,随机抽查了部分女生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图和不完整的统计表(每个分组包括左端点,不包括右端点).请你根据图中提供的信息,解答以下问题:| 仰卧起坐次数的范围(单位:次) | 15~20 | 20~25 | 25~30 | 30~35 | ||||||
| 频数 | 3 | 10 | 12 | |||||||
| 频率 |
|
|
|
| 被抽查的所有女生的仰卧起坐次数的和 |
| 被抽查的所有女生的人数 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com