
题目列表(包括答案和解析)
| 3 |
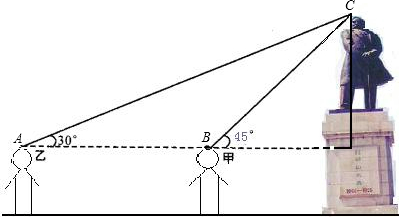
 及到的角度用α、β…表示,最后请给出计算MN的高度的式子).
及到的角度用α、β…表示,最后请给出计算MN的高度的式子).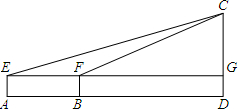 马垅中学有一腾飞小广场,广场中间的石雕上有两只海豚,小明一直想知道它的高度,学了第二十八章《解直角三角形》后,他决定去估测这个建筑的高度.他首先站在A处,测得海豚顶部C的仰角∠CEG=21°,然后他往石雕的方向前进10米到达B处,此时测得仰角∠CFG=37°,已知小明的身高1.5米,请你根据以上的数据帮小明算出该石雕CD的高度(参考数据:sin37°≈
马垅中学有一腾飞小广场,广场中间的石雕上有两只海豚,小明一直想知道它的高度,学了第二十八章《解直角三角形》后,他决定去估测这个建筑的高度.他首先站在A处,测得海豚顶部C的仰角∠CEG=21°,然后他往石雕的方向前进10米到达B处,此时测得仰角∠CFG=37°,已知小明的身高1.5米,请你根据以上的数据帮小明算出该石雕CD的高度(参考数据:sin37°≈| 3 |
| 5 |
| 3 |
| 4 |
| 9 |
| 25 |
| 3 |
| 8 |
| A、0个 | B、1个 | C、2个 | D、3个 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com