练习册

  • 练习册
  • 试题
    3．>(点拨:根据不等式的基本性质.不等式两边同时乘或除以同一个负数.不等号方向改变) 【查看更多】

     

    题目列表(包括答案和解析)

    不等式-6x>12，根据不等式的性质______，不等式两边_______，得x____．

     

    查看答案和解析>>

    28、阅读探究：
    例：如图1，△ABC是等边三角形，点M是边BC的中点，∠AMN=60°，且MN交三角形外角的平分线CN于点N、求证：AM=MN．
    思路点拨：取的AB中点P，连接PM，易证△APM≌△MCQ从而AM=MN．
    问题解决：
    （1）如图2，四边形ABCD是正方形，点M是边BC的中点，CN是正方形ABCD的外角∠DCQ的平分线．
    ①填空：当∠AMN=
    90°
    °时，AM=MN；
    ②证明①的结论．
    （2）请根据例题和问题（1）的解题过程，在正五边形ABCDE中推广出一个类似的真命题．（请在图3中作出相应图形，标注必要的字母，并写出已知和结论，无需证明．）

    查看答案和解析>>

    在直角坐标系中，O为坐标原点. 已知反比例函数y=（k>0）的图象经过点A(2，m)，过点A作AB⊥x轴于点B，且△AOB的面积为.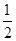
    （1）求k和m的值；
    （2）点C（x，y）在反比例函数y=的图象上，求当1≤x≤3时函数值y的取值范围；
    （3）过原点O的直线l与反比例函数y=的图象交于P、Q两点，试根据图象直接写出线段PQ长度的最小值.

    查看答案和解析>>

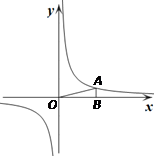
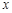    （满分8分）如图，已知直线AB的解析式y=mx+n,它与轴交于点C，与双曲线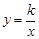交于A（3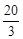，）、B（-5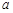，）两点.AD⊥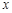轴于点D，BE∥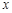轴且与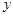轴交于点E.
    （1）求反比例函数的解析式及直线AB的解析式；
    （2）根据函数图象可知，当mx+n->0时，x的取值范围是             ；
    （3）判断四边形CBED的形状，并说明理由.
     

    查看答案和解析>>

    （本题6分）已知函数y＝－x2＋2x－．

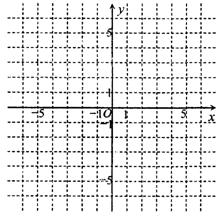
    1.(1)用配方法求它的顶点坐标；

    2.(2)在平面直角坐标系中画出它的简图：

    3.(3)根据图象回答：x取什么值时，y>0．

     

    查看答案和解析>>


    同步练习册答案