（本小题满分8分）在直角坐标系中，已知点A（－2，0）、B（0，4）、C（0，3），过点C作直线交x轴于点D，使得以    D、O、C为顶点的三角形与△AOB相似，求点D的坐标。

（本小题满分5分）已知菱形纸片ABCD的边长为，∠A=60°，E为边上的点，过点E作EF∥BD交AD于点F．将菱形先沿EF按图1所示方式折叠，点A落在点处，过点作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠，点C落在点处，与H分别交与于点M、N．若点在△EF的内部或边上，此时我们称四边形（即图中阴影部分）为“重叠四边形”．

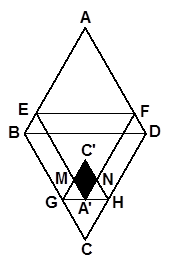
图1                      图2                     备用图

（1）若把菱形纸片ABCD放在菱形网格中（图中每个小三角形都是边长为1的等边三角形），点A、B、C、D、E恰好落在网格图中的格点上．如图2所示，请直接写出此时重叠四边形的面积；

（2）实验探究：设AE的长为，若重叠四边形存在．试用含的代数式表示重叠四边形的面积，并写出的取值范围（直接写出结果，备用图供实验，探究使用）．

（本小题满分6分）

已知：二次函数y=x²+bx+c，其图象对称轴为直线x=1，且经过点（2，–）.

（1）求此二次函数的解析式.

（2）设该图象与x轴交于B、C两点（B点在C点的左侧），请在此二次函数x轴下方的图

象上确定一点E，使△EBC的面积最大，并求出最大面积.

注：二次函数y=x²+bx+c（≠0）的对称轴是直线x=－.

（本小题满分10分）

已知二次函数图象经过，对称轴，抛物线与轴两交点距离为4，求这个二次函数的解析式？

（本小题满分10分）

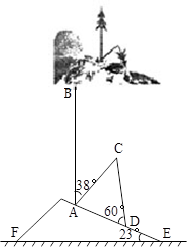2011年3月11日13时46分日本发生了9.0级大地震，伴随着就是海啸。山坡上有一棵与水平面垂直的大树，海啸过后，大树被刮倾斜后折断倒在山坡上，树的顶部恰好接触到坡面（如图所示）。

已知山坡的坡角∠AEF=23°，量得树干的倾斜角为

∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。

（1）求∠DAC的度数；

（2）求这棵大树折点C到坡面AE的距离？

（结果精确到个位，参考数据：，，）．