
题目列表(包括答案和解析)
、(本题8分)如图,CD为⊙O的直径,点A在⊙O上,过点A作⊙O的切线交CD的延长线于点F。已知∠F=30°。
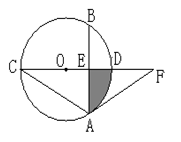
1.(1)求∠C的度数;
2.⑵若点B在⊙O上,AB⊥CD,垂足为E,AB=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
、(本题6分)已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点(1,5)。
的图象相交于点(1,5)。
1.(1)求这两个函数的解析式;
2.(2)求这两个函数图象的另一个交点的坐标。
、为加快西部大开发,某自治区决定新修一条公路,甲、乙两工程队承包此项工程。如果甲工程队单独施工,则刚好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则刚好如期完成。问原来规定修好这条公路需多长时间?
、阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数![]() 发现:如下表
发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1= |
| 3 | 3= |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |
|
③推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即![]()
④结论:![]()
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数![]() ,发现:(填下表)
,发现:(填下表)
| 点的个数 | 可连成三角形个数 |
| 3 |
|
| 4 |
|
| 5 |
|
| …… |
|
| n |
|
(3)推理:
(4)结论:
、形状 的图形叫相似形;两个图形相似,其中一个图形可以看作由另一个图形的 或
而得到的。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com