
题目列表(包括答案和解析)
在实数的原有运算法则中,我们补充新运算法则
“ * ” 如下:当a≥b时,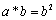 ;当a
< b时,
;当a
< b时,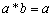 .则当x = 2时,
.则当x = 2时,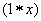 ·
·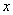
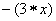 =__________.(“ · ” 和 “ – ”仍为实数运算中的乘号和减号)
=__________.(“ · ” 和 “ – ”仍为实数运算中的乘号和减号)
在实数的原有运算法则中我们补充定义新运算“+”如下:
当a≥b时,a+b=b2;当a<b时,a+b=a。
则当x=2时,(1+x)·x-(3+x)的值为
(“· ”和“-”仍为实数运算中的乘号和减号)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com