
题目列表(包括答案和解析)
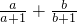 的值.
的值. 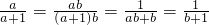
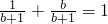
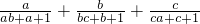 的值.
的值.
 是方程2x3-x2+m=0的解
是方程2x3-x2+m=0的解 )3-(-
)3-(- )2+m=0,即-
)2+m=0,即- -
- +m=0,所以m=
+m=0,所以m=
x1(x1+1)+x2(x2+1)=(x1+1)(x2+1),判断(a+B)2≤4是否正确?若正确,请加以证明;若不正确,请举一反例.
| 第一档电量 | 第二档电量 | 第三档电量 |
| 月用电量210度以下, 每度价格0.52元 |
月用电量210至350度, 每度比第一档提价0.05元 |
月用电量350度以上, 每度电比第一档提价0.30元 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com