
题目列表(包括答案和解析)
已知抛物线L:y=ax2+bx+c(其中a、b、c都不等于0),它的顶点P的坐标是(-![]() ,
,![]() ),与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
),与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
(1)请直接写出抛物线y=2x2-4x+1的伴随抛物线和伴随直线的解析式:
伴随抛物线的解析式________,
伴随直线的解析式________;
(2)若一条抛物线的伴随抛物线和伴随直线分别是y=-x2-3和y=-x-3,则这条抛物线的解析式是________;
(3)求抛物线L:y=ax2+bx+c(其中a、b、c都不等于0)的伴随抛物线和伴随直线的解析式;
(4)若抛物线L与x轴交于A(x1,0),B(x2,0)两点,x2>x1>0,它的伴随抛物线与x轴交于C、D两点,且AB=CD,请求出a、b、c应满足的条件.
如图,抛物线y=-2x2+bx与x轴的两个不同交点是O与A,顶点B在直线y=x上.
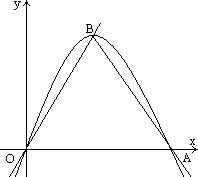
(1)求抛物线的解析式;
(2)证明△OAB是等边三角形;
(3)在抛物线上是否存在点P,使∠OPA=90°?若存在,请求出点P的坐标;若不存在,请说明理由,(抛物线y=ax2+bx+c的顶点坐标是(-![]() ,
,![]() )
)
定义:对于抛物线y=ax2+bx+c ( a、b、c是常数,a≠0),若b2=4ac,则称该抛物线为黄金抛物线.例如:y=2x2-2x+2是黄金抛物线.
(1)请再写出一个与上例不同的黄金抛物线的解析式_ ▲ ;
(2)若抛物线y=ax2+bx+c ( a、b、c是常数,a≠0)是黄金抛物线,请探究该黄金抛物线与x轴的公共点个数的情况(要求说明理由);
(3)将黄金抛物线沿对称轴向下平移3个单位
① 直接写出平移后的新抛物线的解析式;
② 设①中的新抛物线与y轴交于点A,对称轴与x轴交于点B,动点Q在对称轴上,问新抛物线上是否存在点P,使以点P、Q、B为顶点的三角形与△AOB全等?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由
【提示:抛物线y=ax2+bx+c (a≠0)的对称轴是x=-![]() ,顶点坐标是 (-
,顶点坐标是 (-![]() ,
,![]() )】
)】


如图,已知抛物线y=2x2-4x+m与x轴交于不同的两点A、B,其顶点是C,点D是抛物线的对称轴与x轴的交点.

(1)求实数m的取值范围;
(2)求顶点C的坐标和线段AB的长度(用含有m的式子表示);
(3)若直线![]() 分别交x轴、y轴于点E、F,问△BDC与△EOF是否有可能全等,如果可能,请证明;如果不可能,请说明理由.
分别交x轴、y轴于点E、F,问△BDC与△EOF是否有可能全等,如果可能,请证明;如果不可能,请说明理由.
如图所示,已知二次函数y=2x2-2的图象与x轴交于点A,B两点(点A在点B左侧)与y轴交于点C,直线x=m(m>1)与x轴交于点D.
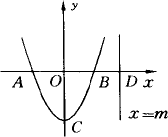
(1)求A,B,C三点坐标;
(2)在直线x=m(m>1)上有一点P(点P在第一象限),使得以P,D,B为顶点的三角形与以B,C,O为顶点的三角形相似,求P点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,试问抛物线y=2x2-2上是否存在一点Q使得四边形ABPQ为平行四边形?如果存在这样的点Q,请求出m的值;如果不存在,简要说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com