26、一辆邮政车自A城驶往B城，沿途有n个车站（包括起点A和终点B），行驶时需要在每个车站停靠，每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个，还要装上该站发给后面行程中每个车站的邮包一个．例如，当邮车停靠在第x个车站时，需要卸下已经通过的（x-1） 个车站发给该站的邮包（x-1）个，还要装上后面行程中要停靠的（n-x）个车站的邮包（n-x）个．
（1）沿途有4个车站（n=4），邮政车在各个车站启程时邮包的总个数为：
在第1个车站（x=1）启程时邮包的总个数：3．
在第2个车站（x=2）启程时邮包的总个数：3-1+2=4．
在第3个车站（x=3）启程时邮包的总个数为：
4-2+1=3
．
（2）沿途有n个车站，邮政车在各个车站启程时邮包的总个数为：
在第1个车站（x=1）启程时邮包的总个数：n-1．
在第2个车站（x=2）启程时邮包的总个数：（n-1）-1+（n-2）=2n-4．
依照上述做法，解答下列问题：
①求在第3个车站（x=3）启程时邮包的总个数（应仿照x=2的做法，不能只写最后的结果）；
②猜想在第k个车站（x=k）启程时邮包的总个数（用含n，k的代数式表示，可直接写出最后的结果）．
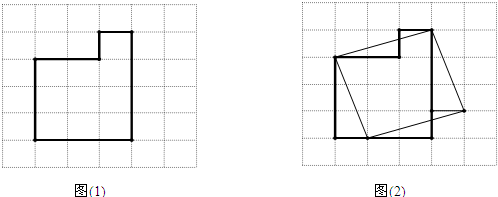
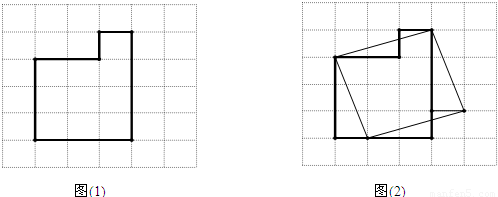
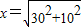．由此可知正方形的边长等于两个直角边分别为30cm和10cm的直角三角形斜边的长．于是，画出如图（2）所示的正方形．