下列说法正确的是

1. A.
   若a为有理数，则a²＞0
2. B.
   两个相反数的绝对值相等
3. C.
   任何数的偶次幂都是正数
4. D.
   若a为任意有理数，则10a＞9a

请认真阅读题意，并根据你的发现填空：
（1）将任何一组已知的勾股数中的每一个数都扩大为原来的正整数倍后，就得到一组新的勾股数，例如：3、4、5，我们把每一个数扩大为原来的2倍、3倍，则分别得到6、8、10和9、12、15，
若把每一个数都扩大为原来的12倍，就得到______________，
若把每一数都扩大为原来的n（n为正整数）倍，则得到_________________；
（2）对于任意一个大于1的奇数，存在着下列勾股数
若勾股数为3、4、5.   则有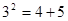
若勾股数为5、12、13， 则有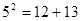
若勾股数为7、24、25， 则有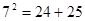
若勾股数为m（m为奇数）、n、______
则有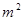=2n+1，用m表示n=_______
当m=17时，n=_______，此时勾股数为_______________.

请认真阅读题意，并根据你的发现填空：

（1）将任何一组已知的勾股数中的每一个数都扩大为原来的正整数倍后，就得到一组新的勾股数，例如：3、4、5，我们把每一个数扩大为原来的2倍、3倍，则分别得到6、8、10和9、12、15，

若把每一个数都扩大为原来的12倍，就得到______________，

若把每一数都扩大为原来的n（n为正整数）倍，则得到_________________；

（2）对于任意一个大于1的奇数，存在着下列勾股数

若勾股数为3、4、5.   则有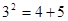

若勾股数为5、12、13， 则有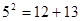

若勾股数为7、24、25， 则有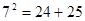

若勾股数为m（m为奇数）、n、______

则有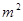=2n+1，用m表示n=_______

当m=17时，n=_______，此时勾股数为_______________.

阅读下列材料：

　 我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离；即，也就是说，|x|表示在数轴上数x与数0对应点之间的距离；

这个结论可以推广为表示在数轴上，对应点之间的距离；

例1 解方程，容易看出，在数轴下与原点距离为2点的对应数为±2，即该方程的解为x=±2

例2 解不等式▏x-1▏＞2，如图，在数轴上找出_▏x-1▏=2的解，即到1的距离为2的点对应的数为－1、3，则▏x-1▏＞2的解为x<－1或x>3

例3 解方程。由绝对值的几何意义知，该方程表示求在数轴上与1

和－2的距离之和为5的点对应的x的值。在数轴上，1和－2的距离为3，满足方程的x对应点在1的右边或－2的左边，若x对应点在1的右边，由图可以看出x＝2；同理，若x对应点在－2的左边，可得x＝－3，故原方程的解是x=2或x=－3

参考阅读材料，解答下列问题：

（1）方程的解为　　　　　　　　　　

（2）解不等式≥9；

（3）若≤a对任意的x都成立，求a的取值范围.

我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离；即，也就是说，|x|表示在数轴上数x与数0对应点之间的距离；

 这个结论可以推广为表示在数轴上，对应点之间的距离；

例1:解方程，容易看出，在数轴下与原点距离为2点的对应数为±2，即该方程的解为x=±2

例2:解不等式▏x-1▏＞2，如图，在数轴上找出▏x-1▏=2的解，即到1的距离为2的点对应的数为－1、3，则▏x-1▏＞2的解为x<－1或x>3

例3:解方程。由绝对值的几何意义知，该方程表示求在数轴上与1

和－2的距离之和为5的点对应的x的值。在数轴上，1和－2的距离为3，满足方程的x对应点在1的右边或－2的左边，若x对应点在1的右边，由图可以看出x＝2；同理，若x对应点在－2的左边，可得x＝－3，故原方程的解是x=2或x=－3

参考阅读材料，解答下列问题：

（1）方程的解为                     

（2）解不等式≥9；

（3）若≤a对任意的x都成立，求a的取值范围.