题目列表(包括答案和解析)
新星电子科技公司积极应对2008年世界金融危机，及时调整投资方向，瞄准光伏产业，建成了太阳能光伏电池生产线．由于新产品开发初期成本高，且市场占有率不高等因素的影响，产品投产上市一年来，公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次)．公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上．该图象从左至右，依次是线段OA、曲线AB和曲线BC，其中曲线AB为抛物线的一部分，点A为该抛物线的顶点，曲线BC为另一抛物线y＝－5x2＋205x－1230的一部分，且点A，B，C的横坐标分别为4，10，12
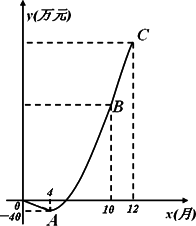
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式；
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程)；
(3)前12个月中，第几个月该公司所获得的利润最多？最多利润是多少万元？
使得函数值为零的自变量的值称为函数的零点．例如，对于函数，
令y＝0，可得x＝1，我们就说1是函数的零点．己知函数 (m为常数)．
（1）当
＝0时，求该函数的零点；
（2）证明：无论取何值，该函数总有两个零点；
（3）如图，设函数的两个零点分别为
和
，且
，此时函数图象与x轴的交点分别为A、B(点A在点B左侧)，点M在直线
上，当MA＋MB最小时，求直线AM的函数解析式．
为实现沈阳市森林城市建设的目标，在今年春季的绿化工作中，绿化办计划为某住宅小区购买并种植400株树苗．某树苗公司提供如下信息：
信息一：可供选择的树苗有杨树、丁香树、柳树三种，并且要求购买杨树、丁香树的数量相等．
信息二：如下表：
设购买杨树、柳树分别为x株、y株．
(1)写出y与x之间的函数关系式(不要求写出自变量的取值范围)；
(2)当每株柳树的批发价P等于3元时，要使这400株树苗两年后对该住宅小区的空气净化指数不低于90，应怎样安排这三种树苗的购买数量，才能使购买树苗的总费用最低？最低的总费用是多少元？
(3)当每株柳树批发价格P(元)与购买数量y(株)之间存在关系P＝3－0.005y时，求购买树苗的总费用W(元)与购买杨树数量x(株)之间的函数关系式(不要求写出自变量的取值范围)．
使得函数值为零的自变量的值称为函数的零点．例如，对于函数y＝x－1，令y＝0，可得x＝1，我们就说1是函数y＝x－1的零点．请根据零点的定义解决下列问题：已知函数y＝x2－2mx－2(m＋3)(m为常数)．
(1)当m＝0时，求该函数的零点；
(2)证明：无论m取何值，该函数总有两个零点；
(3)设函数的两个零点分别为x1和x2，且
，此时函数图象与x轴的交点分别为A、B(点A在点B左侧)，点M在直线y＝x－10上，当MA＋MB最小时，求直线AM的函数解析式．
（本题满分12分）如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b
与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=
，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．
(1)OH的长度等于___________；k＝___________，b＝____________；
(2)是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶
点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜
，写出探索过程．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com