43．设抛物线y=ax2+bx+c经过A两点.且与y轴相交于点M． (1)求b和c,(2)在抛物线y=ax2-bx+c-1上横坐标与纵坐标相等的点的坐标,小题所求出的点中.有一个点也在抛物线y=ax2——青夏教育精英家教网—

43．设抛物线y=ax2+bx+c经过A两点.且与y轴相交于点M． (1)求b和c,(2)在抛物线y=ax2-bx+c-1上横坐标与纵坐标相等的点的坐标,小题所求出的点中.有一个点也在抛物线y=ax2+bx+c上.试判断直线AM和x轴的位置关系.并说明理由．【查看更多】

题目列表(包括答案和解析)

设抛物线y＝ax²＋bx＋c经过A(－1，2)，B(2，－1)两点，且与y轴交于点M．

(1)求b和c(用含a的代数式表示)；

(2)求抛物线y＝ax²－bx＋c－1上横坐标与纵坐标相等的点的坐标；

(3)在第(2)小题所求出的点中，有一个点也在抛物线y＝ax²＋bx＋c上，试判断直线AM和x轴的位置关系，并说明理由．

已知抛物线C₁的函数解析式为y＝ax²＋bx－3a（b＜0），若抛物线C₁经过点（0，－3），方程ax²＋bx－3a＝0的两根为x₁，x₂，且|x₁－x₂|＝4.

⑴求抛物线C₁的顶点坐标. 新课标第一网

⑵已知实数x＞0，请证明x＋≥2，并说明x为何值时才会有x＋＝2.

⑶若将抛物线先向上平移4个单位，再向左平移1个单位后得到抛物线C₂，设A（m，y₁），B（n，y₂）是C₂上的两个不同点，且满足：∠AOB＝90︒，m＞0，n＜0.请你用含m的表达式表示出△AOB的面积S，并求出S的最小值及S取最小值时一次函数OA的函数解析式.

（参考公式：在平面直角坐标系中，若P（x₁，y₁），Q（x₂，y₂），则P，Q两点间的距离为）

如图，已知点B(1，3)、C(1，0)，直线y＝x＋k经过点B，且与x轴交于点A，将△ABC沿直线AB折叠得到△ABD．

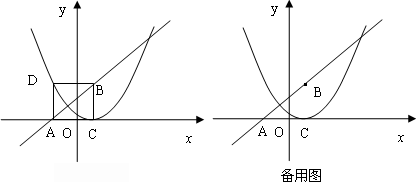
(1)填空：A点坐标为(____，____)，D点坐标为(____，____)；

(2)若抛物线y＝x²＋bx＋c经过C、D两点，求抛物线的解析式；

(3)将(2)中的抛物线沿y轴向上平移，设平移后所得抛物线与y轴交点为E，点M是平移后的抛物线与直线AB的公共点，在抛物线平移过程中是否存在某一位置使得直线EM∥x轴．若存在，此时抛物线向上平移了几个单位？若不存在，请说明理由．

(提示：抛物线y＝ax²＋bx＋c(a≠0)的对称轴是x＝－，顶点坐标是(－，)

如图，已知点B(1，3)、C(1，0)，直线y＝x＋k经过点B，且与x轴交于点A，将△ABC沿直线AB折叠得到△ABD．

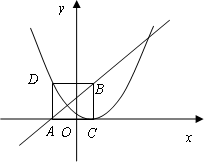
(1)填空：A点坐标为(________，________)，D点坐标为(________，________)；

(2)若抛物线y＝x²＋bx＋c经过C、D两点，求抛物线的解析式；

(提示：抛物线y＝ax²＋bx＋c(a≠0)的对称轴是x＝－，顶点坐标是(－，)

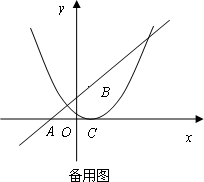
如图所示，已知：抛物线y＝ax²＋bx＋c(a≠0)经过x轴上的两点A(x₁，0)、B(x₂，0)和y轴上的点C(0，－)，⊙P的圆心P在y轴上，且经过B、C两点，b＝a，AB＝2．

(1)求抛物线的解析式；

(2)D在抛物线上，且C、D两点关于抛物线的对称轴对称，直线BD是否经过圆心P？请说明理由．

(3)设直线BD交⊙P于另一点E，求经过E点的⊙P的切线的解析式．

同步练习册答案