
题目列表(包括答案和解析)
如果二次函数y=ax2+bx+c 的图象的顶点是(-2,4),且过点(-3,0),则a为_____________.
若x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1,x2和系数a,b,c有如下关系:x1+x2=-![]() ,x1·x2=
,x1·x2=![]() .我们把它们称为根与系数关系定理.
.我们把它们称为根与系数关系定理.
如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
AB=|x1-x2|=![]() =
=![]() =
=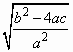 =
=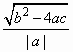 .
.
请你参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点为A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值;
如图,矩形![]() 是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的.
是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的.![]() 点在x轴的正半轴上,B点的坐标为(1,3).
点在x轴的正半轴上,B点的坐标为(1,3).
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O、![]() 两点且图象顶点M的纵坐标为-1.求这个二次函数的解析式;
两点且图象顶点M的纵坐标为-1.求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点P,使得ΔPOM为直角三角形?若存在,请求出P点的坐标和ΔPOM的面积;若不存在,请说明理由;
(3)求边![]() 所在直线的解析式.
所在直线的解析式.
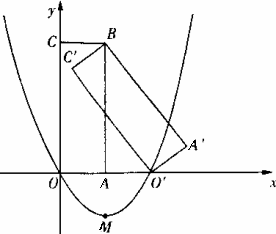
如图,矩形![]() 是由矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,
是由矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,![]() 点在x轴的正半轴上,B点的坐标为(1,3).
点在x轴的正半轴上,B点的坐标为(1,3).![]() 与AB交于D点.
与AB交于D点.
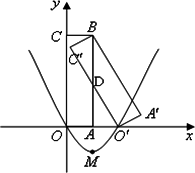
(1)求D点的坐标;
(2)如果二次函数y=ax2+bx+c(a≠0)的图象经过点O、![]() 两点且图象顶点M的纵坐标为-1,求这个二次函数的解析式;
两点且图象顶点M的纵坐标为-1,求这个二次函数的解析式;
(3)若将直线OC绕点O旋转α度(0<α<90)后与抛物线的另一个交点为P,则以O、![]() 、B、P为顶点的四边形能否是平行四边形?若能,求出tanα的值;若不能,请说明理由.
、B、P为顶点的四边形能否是平行四边形?若能,求出tanα的值;若不能,请说明理由.
如图,矩形![]() 是矩形ABCO绕点B顺时针旋转得到的.其中点
是矩形ABCO绕点B顺时针旋转得到的.其中点![]() ,C在x轴负半轴上,线段OA在y轴正半轴上,B点的坐标为(-1,3).
,C在x轴负半轴上,线段OA在y轴正半轴上,B点的坐标为(-1,3).
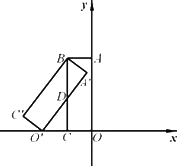
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O、![]() 两点且图象顶点M的纵坐标为-1.求这个二次函数的解析式;
两点且图象顶点M的纵坐标为-1.求这个二次函数的解析式;
(2)求边![]()
![]() 所在直线的解析式;
所在直线的解析式;
(3)在(1)中求出的二次函数图象上是否存在点P,使得![]() ,若存在,请求出点P的坐标,若不存在,请说明理由.
,若存在,请求出点P的坐标,若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com