练习册

  • 练习册
  • 试题
    33．已知等边△ABC和点P.设点P到△ABC三边AB.AC.BC的距离分别为h1.h2.h3.△ABC的高为h. “若点P在一边BC上.此时h3=0,可得结论h1+h2+h3＝h 请直接应用上述信息解决下列问题: 当点P在△ABC内.点P在△ABC外这两种情况时.上述结论是否还成立?若成立.请给予证明,若不成立.h1.h2.h3与h之间的关系如何?请写出你的猜想.不需证明. 【查看更多】

     

    题目列表(包括答案和解析)

    已知等边△ABC和点P，设点P到△ABC三边AB，AC，BC的距离分别为h1，h2，h3，△ABC的高为h．

    “若点P在一边BC上(图①)，此时h＝0，可得结论：h1＋h2＋h3＝h．

    请直接应用上述信息解决下列问题：

    当点P在△ABC内(图②)、点P在△ABC外(图③)这两种情况时，上述结论是否成立？若成立，请给予证明；若不成立，h1，h2，h3与h之间又有怎样的关系？请写出你的猜想，不需证明．

    查看答案和解析>>

    如图，已知△ABC是边长为6cm的等边三角形，动点P，Q同时从A、B两点出发，分别沿AB、BC方向精英家教网匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q运动到点C时，P，Q都停止运动．
    （1）出发后运动2s时，试判断△BPQ的形状，并说明理由；那么此时PQ和AC的位置关系呢？请说明理由；
    （2）设运动时间为t，△BPQ的面积为S，请用t的表达式表示S．

    查看答案和解析>>

    如图，已知△ABC是边长为6cm的等边三角形，动点P，Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q运动到点C时，P，Q都停止运动．
    （1）出发后运动2s时，试判断△BPQ的形状，并说明理由；那么此时PQ和AC的位置关系呢？请说明理由；
    （2）设运动时间为t，△BPQ的面积为S，请用t的表达式表示S．

    查看答案和解析>>

    如图，已知△ABC三边长相等，和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h，在图①中，点P是边BC的中点，由得，AB·h1+AC·h2=BC·h，可得h1+h2=h，又因为h3=0，所以：h1+h2+h3=h。图②～⑤中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外。
    （1）请探究：图②～⑤中，h1、h2、h3、h之间的关系；（直接写出结论）
    （2）说明图③所得结论为什么是正确的；
    （3）说明图⑤所得结论为什么是正确的。

    查看答案和解析>>

    已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3，△ABC的高为h．“若点P在一边BC上(如图①)，此时h3＝0，可得结论：h1＋h2＋h3＝h．”请直接应用上述信息解决下列问题：

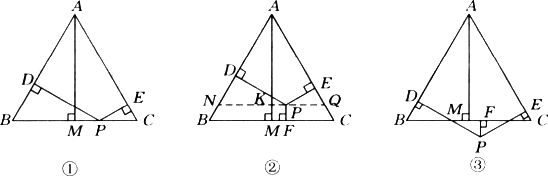
    当点P在△ABC内(如图②)、点P在△ABC外(如图③)这两种情况时，上述结论是否还成立？若成立，请说明理由；若不成立，h1、h2、h3与h之间又有怎样的关系？请写出你的猜想，不需说明理由．

    查看答案和解析>>


    同步练习册答案