练习册

  • 练习册
  • 试题
    略解:利用角平分线的性质.构造直角三角形:作CE⊥AB于E.CF⊥AD于F.易证CEB≌△CFD.则有EB＝FD,又可证△CEA≌△CFA.于是由 AE＝AF 可得21-EB＝9+FD.∴ EB＝FD＝6, 在Rt△AFC中.有AC＝ ＝. 【查看更多】

     

    题目列表(包括答案和解析)

    育新中学校园内有一块直角三角形（Rt△ABC）空地，如图所示，园艺师傅以角平分线AD为界，在其两侧分别种上了不同的花草，在△ABD区域内种植了一串红，在△ACD区域内种植了鸡冠花，并量得两直角边AB=20m，AC=10m，求一串红与鸡冠花两种花草各种植的面积（提示：利用角平分线的性质）

    查看答案和解析>>

    6、利用角平分线的性质，找到△ABC内部距三边距离相等的点．

    查看答案和解析>>

    如图，OB、OC分别为∠ABC，∠ACB的平分线，∠BOC随着∠A的变化而变化．为探究∠A和∠BOC的关系，现采取如下两种方案，在变化过程中，设∠A为x°，∠BOC为y°．
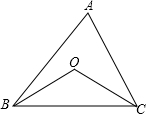
    方案甲：用量角器量出∠A、∠BOC的不断变化时的具体数据，并列表如下：精英家教网
    x 10 20 30 40 …
    y 95 100 105 110 …
    建立直角坐标系，并描点、连线，猜测y与x之间的函数关系，求出y与x的函数关系式．
    方案乙：利用角平分线的性质及三角形内角和为180°的性质，直接进行计算，求出y与x之间的函数关系．
    （1）若x=60°，则y=
     
    ．（请直接写精英家教网出结果）
    （2）请采用方案甲或方案乙中的一种进行解答，得到∠A与∠BOC之间的关系．

    查看答案和解析>>

    利用角平分线的性质，找到△ABC内部距三边距离相等的点.

     

    查看答案和解析>>

    利用角平分线的性质，找到△ABC内部距三边距离相等的点．

    查看答案和解析>>


    同步练习册答案