
题目列表(包括答案和解析)
如图,在矩形ABCD中,AB=12厘米,BC=6厘米.点P沿AB边从A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么:
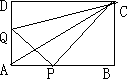
(1)当t为何值时,⊿QAP为等腰直角三角形?
(2)求四边形QPAC的面积;提出一个与计算结果有关的结论;
(3)当t为何值时,以点Q、A、P为顶点的三角形与⊿ABC相似?
如图1,在矩形ABCD中,AB=12厘米,BC=6厘米,点P从A点出发,沿A →B→C→D路线运动,到D点停止;点Q从D点出发,沿D →C →B →A运动,到A点停止.若点P,点Q同时出发,点P的速度为每秒1厘米,点Q的速度为每秒2厘米,a秒时点P,点Q同时改变速度,点P的速度变为每秒b厘米,点Q的速度变为每秒c厘米.如图2是描述点P出发x秒后△APD的面积S1()与x(秒)的函数关系的图象.图3是描述点Q出发x秒后△AQD的面积S2(
)与x(秒)的函数关系图象.根据图象:
(1)求a、b、c的值;
(2)设点P离开点A的路程为y1(厘米),点Q到点A还需要走的路程为y2(厘米),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式,并求出P与Q相遇时x的值.
如图1,在矩形ABCD中,AB=12厘米,BC=6厘米,点P从A点出发,沿A →B→C→D路线运动,到D点停止;点Q从D点出发,沿D →C →B →A运动,到A点停止.若点P,点Q同时出发,点P的速度为每秒1厘米,点Q的速度为每秒2厘米,a秒时点P,点Q同时改变速度,点P的速度变为每秒b厘米,点Q的速度变为每秒c厘米.如图2是描述点P出发x秒后△APD的面积S1( )与x(秒)的函数关系的图象.图3是描述点Q出发x秒后△AQD的面积S2(
)与x(秒)的函数关系的图象.图3是描述点Q出发x秒后△AQD的面积S2( )与x(秒)的函数关系图象.根据图象:
)与x(秒)的函数关系图象.根据图象:

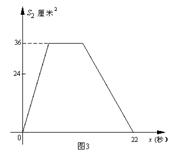
(1)求a、b、c的值;
(2)设点P离开点A的路程为y1(厘米),点Q到点A还需要走的路程为y2(厘米),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式,并求出P与Q相遇时x的值.
如图,矩形
ABCD中,AB=8厘米,BC=12厘米,P、Q分别是AB、BC上运动的两点.若点P自点A出发,以1厘米/秒的速度沿AB方向运动,同时点Q自点B出发以2厘米/秒的速度沿BC方向运动.设点P运动的时间为t秒,当t为何值时,以P、B、Q为顶点的三角形与△BCD相似?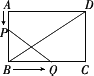
已知:矩形纸片ABCD中,AB=26厘米,BC=18.5厘米,点E在AD上,且AE=6厘米,点P是![]() 边上一动点.按如下操作:
边上一动点.按如下操作:
步骤一,折叠纸片,使点P与点![]() 重合,展开纸片得折痕MN(如图23(1)所示);
重合,展开纸片得折痕MN(如图23(1)所示);
步骤二,过点P作![]() ,交MN所在的直线于点Q,连接QE(如图23(2)所示)
,交MN所在的直线于点Q,连接QE(如图23(2)所示)
(1)无论点P在![]() 边上任何位置,都有PQ QE(填“
边上任何位置,都有PQ QE(填“![]() ”、“
”、“![]() ”、“
”、“![]() ”号);
”号);
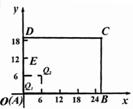
(2)如图23(3)所示,将纸片ABCD放在直角坐标系中,按上述步骤一、二进行操作:
①当点![]() 在
在![]() 点时,PT与MN交于点Q1 ,Q1点的坐标是( , );
点时,PT与MN交于点Q1 ,Q1点的坐标是( , );
②当PA=6厘米时,PT与MN交于点Q2 ,Q2点的坐标是( , );
③当PA=12厘米时,在图22(3)中画出MN,PT(不要求写画法),并求出MN与PT的交点Q3的坐标;
(3)点![]() 在运动过程中,PT与MN形成一系列的交点Q1 ,Q2 ,Q3 ,…观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
在运动过程中,PT与MN形成一系列的交点Q1 ,Q2 ,Q3 ,…观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
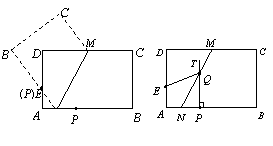 |
23(1) 23(2) 23(3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com