
题目列表(包括答案和解析)
在形如 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果 (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:  ,例如:求
,例如:求 ,因为
,因为 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ 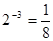 ,∴
,∴  .
.
1.根据定义计算:(本小题6分)
① =____;②
=____;② =
;
=
;
③如果 ,那么x= 。
,那么x= 。
2.设 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),
∵ ,∴
,∴ ∴
∴ ,
,
即
这是对数运算的重要性质之一,进一步,我们还可以得出:
 =
.(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
=
.(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
3.请你猜想: (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)
在形如![]() 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果![]() (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ![]() ,例如:求
,例如:求 ,因为
,因为 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ ![]() ,∴
,∴ ![]() .
.
1.根据定义计算:(本小题6分)
① =____;②
=____;② = ;
= ;
③如果![]() ,那么x= 。
,那么x= 。
2.设 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),
∵![]() ,∴
,∴![]() ∴
∴ ,
,
即
这是对数运算的重要性质之一,进一步,我们还可以得出:
 = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
3.请你猜想: (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)
 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算; (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ,例如:求
,例如:求 ,因为
,因为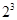 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ ,∴
,∴ .
. =____;②
=____;② = ;
= ; ,那么x= 。
,那么x= 。 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数), ,∴
,∴ ∴
∴ ,
,
 = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分) (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)某人去水果批发市场采购苹果,他看中了A、B两家苹果。这两家苹果品质一样,零售价都为6元/千克,批发价各不相同。
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠。
B家的规定如下表:

【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】
1.(1)如果他批发600千克苹果,则他在A家批发需要_____________元,在B家批发需要
_________元;
2. (2)如果他批发x千克苹果(1500<![]() <2000),则他在A家批发需要__________元,在B 家批发需要________元(用含x的代数式表示);
<2000),则他在A家批发需要__________元,在B 家批发需要________元(用含x的代数式表示);
3. (3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由。(本小题7分)
(本小题10分)在等腰梯形ABCD中,AD∥BC,且AD=2,以CD为直径作⊙
O1,交BC于点E,过点E作EF⊥AB于F,建立如图12所示的平面直角坐标系,已知A,
B两点的坐标分别为A(0,2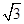 ),B(-2,0).
),B(-2,0).
(1)求C,D两点的坐标.
(2)求证:EF为⊙O1的切线.
(3)探究:如图13,线段CD上是否存在点P,使得线段PC的长度与P点到y轴的距离相等?如果存在,请找出P点的坐标;如果不存在,请说明理由.
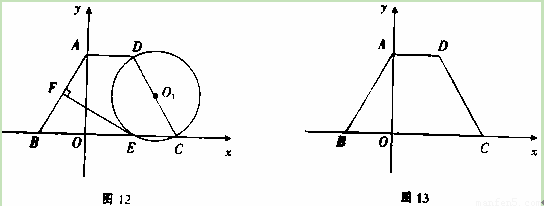
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com