
题目列表(包括答案和解析)
1. (本题满分9分) 某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就不得奖,并罚唱一首歌.
1.(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是 .
2.(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
(本题满分10分)
张先生前年在美美家园住宅小区订购了一套住房,图纸如图所示。已知:①该住房的价格![]() 元/平方米;②楼层的电梯、楼梯及门厅前室面积由两户购房者平均负担;③每户配置车库16平方米,每平方米以6000元计算;
元/平方米;②楼层的电梯、楼梯及门厅前室面积由两户购房者平均负担;③每户配置车库16平方米,每平方米以6000元计算;
根据以上提供的信息和数据计算:
(1)张先生这次购房总共应付款多少元?
(2)若经过两年,该住房价格变为21600元/平方米,那么该小区房价的年平均增长率为多少?
(3)张先生打算对室内进行装修,甲、乙两公司推出不同的优惠方案:在甲公司累计购买10000元材料后,再购买的材料按原价的90%收费;在乙公司累计购买5000元材料后,再购买的材料按原价的95%收费.张先生怎样选择能获得更大优惠?

(本题满分10分)
“教师节”快要到了,张爷爷欲用120元钱,为“光明”幼儿园购买价格分别为8元、6元和5元的图书20册.
1.(1)若设8元的图书购买 册,6元的图书购买
册,6元的图书购买 册,求
册,求 与
与 之间的函数关系式.
之间的函数关系式.
2.(2)若每册图书至少购买2册,求张爷爷有几种购买方案?并写出 取最大值和
取最大值和 取最小值时的购买方案.
取最小值时的购买方案.
1. (本题满分9分) 某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就不得奖,并罚唱一首歌.
1.(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是 .
2.(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
(本题满分10分)张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙,另三边用总长
为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形
ABCD的面积为S平方米.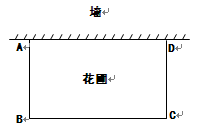
【小题1】(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)
【小题2】(2)当x为何值时,S有最大值?并求出最大值.
(参考公式:二次函数 (
( ),当
),当 时,
时,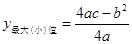 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com