
题目列表(包括答案和解析)
| 3 | x |
如图,网格中每个小正方形的边长为1,请你认真观察图(1)的三个网格中阴影部分构成的图案,解答下列问题:
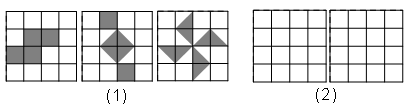
这三个图案都具有以下共同特征:都是 ▲ 对称图形,面积都是 ▲ ;
⑵ 请在图(2)中设计出2个具备上述特征而且不是轴对称图形的图案,要求所画图案不能
与图(1)中给出的图案相同.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com