
题目列表(包括答案和解析)
(本题满分14分)
如图,在![]() 中,
中,![]() ,
,![]() 是斜边
是斜边![]() 上的中线,
上的中线,![]() ,
,![]() ,点
,点![]() 是
是![]() 延长线上的一动点,过点
延长线上的一动点,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
设![]() .
.

1.(1)求![]() 关于
关于![]() 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)
2.(2)联结![]() ,当
,当![]() 平分
平分![]() 时,求
时,求![]() 的长;(4分)
的长;(4分)
3.(3)过点![]() 作
作![]() 交
交![]() 于
于![]() ,当
,当![]() 和
和![]() 相似时,求
相似时,求![]() 的值.(6分)
的值.(6分)
(本题满分14分)如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
⑴如图②,若M为AD边的中点,①△AEM的周长=____ _cm;②求证:EP=AE+DP;

⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.

(本题满分14分)
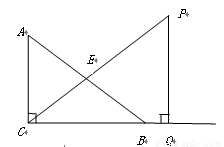
如图,在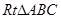 中,
中,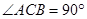 ,
, 是斜边
是斜边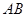 上的中线,
上的中线,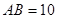 ,
,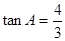 ,点
,点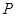 是
是 延长线上的一动点,过点
延长线上的一动点,过点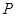 作
作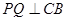 ,交
,交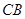 延长线于点
延长线于点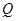 ,
,
设 .
.
1.(1)求 关于
关于 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)
2.(2)联结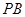 ,当
,当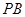 平分
平分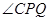 时,求
时,求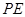 的长;(4分)
的长;(4分)
3.(3)过点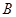 作
作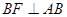 交
交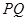 于
于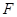 ,当
,当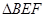 和
和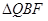 相似时,求
相似时,求 的值.(6分)
的值.(6分)
(本题满分14分)如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A
 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
(1)求直线AC的解析式;
(2)设△PQC的面积为S,求S关于t的函数解析式;
(3)在y轴上找一点M,使△MAC和△MBC都是等
腰三角形。直接写出所有满足条件的M点的坐标;
(4)过点P作PE⊥AC,垂足为E,当P点运动时,
线段EG的长度是否发生改变,请说明理由。
(本题满分14分)如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A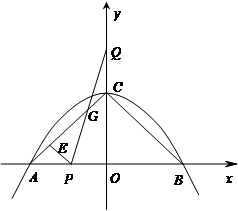 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
(1)求直线AC的解析式;
(2)设△PQC的面积为S,求S关于t的函数解析式;
(3)在y轴上找一点M,使△MAC和△MBC都是等
腰三角形。直接写出所有满足条件的M点的坐标;
(4)过点P作PE⊥AC,垂足为E,当P点运动时,
线段EG的长度是否发生改变,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com