（本小题10分）

抛物线经过点O（0，0），A（4，0），B（2，2）．

（1）求该抛物线的解析式；

（2）画出此抛物线的草图；

（3）求证：△AOB是等腰直角三角形；

（4）将△AOB绕点O按顺时针方向旋转135°得△，写出边的中点P的   坐标，试判定点P是否在此抛物线上，并说明理由．

（本小题10分）求下列代数式的值

1.（1）若a=—2，b=—3，则代数式(a+b)²—(a—b)²=___________

2.（2）当x—y=3时，代数式2(x—y)²+3x—3y+1=___________

3.（3）化简并求值：已知三个有理数的积是负数，其和为正数；当时，求代数式的值。

（本小题10分）在等腰梯形ABCD中，AD∥BC，且AD=2，以CD为直径作⊙
O₁，交BC于点E，过点E作EF⊥AB于F，建立如图12所示的平面直角坐标系，已知A，
B两点的坐标分别为A(0，2)，B(-2，0).
（1）求C，D两点的坐标.
（2）求证：EF为⊙O₁的切线.
（3）探究：如图13，线段CD上是否存在点P，使得线段PC的长度与P点到y轴的距离相等？如果存在，请找出P点的坐标；如果不存在，请说明理由.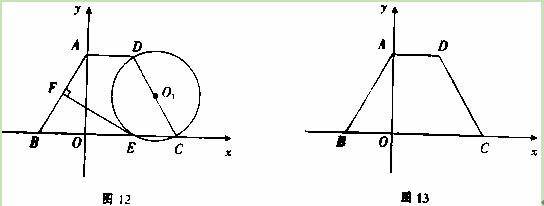

（本小题10 分），某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个，摆放在迎宾大道两侧．已知搭配一个A种造型需甲种花卉8盆，乙种花卉4盆；搭配一个B种造型需甲种花卉5盆，乙种花卉9盆．

(l）某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来；

(2）若搭配一个A种造型的成本是200元，搭配一个B种造型的成本是360元，试说明（1）中哪种方案成本最低，最低成本是多少元？

（本小题10分）如图11，已知二次函数y= -x² +mx +4m的图象与x轴交于

A(x₁，0)，B(x₂，0)两点(B点在A点的右边)，与y轴的正半轴交于点C，且(x₁+x₂) - x₁x₂=10.

（1）求此二次函数的解析式.

（2）写出B，C两点的坐标及抛物线顶点M的坐标；

（3）连结BM，动点P在线段BM上运动（不含端点B，M），过点P作x轴的垂线，垂足为H，设OH的长度为t，四边形PCOH的面积为S.请探究：四边形PCOH的面积S有无最大值？如果有，请求出这个最大值；如果没有，请说明理由.